[RL] From $r$ to $Q^*$: Your Language Model is Secretly a Q-Function
[RL] From $r$ to $Q^*$: Your Language Model is Secretly a Q-Function
- paper: https://arxiv.org/pdf/2404.12358
- github: X
- COLM 2024 accepted (인용수: 136회, ‘25-07-10 기준)
- downstream task:
1. Motivation
- DPO (Direct Preference Optimization)이 RLHF (Reinforcement Learning with Human Feedback)의 대체안으로 등장하였다.
- 하지만 DPO와 RLHF는 misalignment 이슈가 있었다.
- RLHF는 token-level의 MDP (Markov Decision Process)인 반면,
- DPO는 전체 응답을 하나의 arm으로 표현하는 Contextual Bandid 문제로 치환한다.
- Contextual Bandid?
- Contextual: 문맥, 여기서는 입력으로 제공하는 Instruction에 해당
- Bandid: 도박 슬롯머신의 땡기는 arm에서 파생된 용어로, 여기서는 전체 응답을 하나의 arm으로 표현
- Contextual Bandid?
$\to$ DPO를 RLHF의 token-level MDP로 바라보는 새로운 접근법을 제안해보자!
2. Contribution
-
DPO를 LLM의 binary preference-feedback기반의 token-level MDP setting로 볼수 있는 새로운 시각을 제안한다.
- LLM의 logit이 expected future reward인 optimal Q function으로 정의됨을 보임으로써
- DPO 학습이 token-level reward function을 내재적으로 학습함
-
유도한 이론적 결과를 뒷받침할 3가지 실제적인 통찰력 제공함
-
DPO 학습이 contextual bandit로 학습했음에도 (sparse reward), per-token interpretation이 가능함을 보임
-
DPO기반의 likelihood search 방식이 최신 연구들에서 보인 reward function기반의 decoding과정과 같음을 보임
- 초기 policy & reference를 선택하는게 implicit reward의 trajectory 결정에 중요함을 보임
-
3. From $r$ to $Q^*$
3.1 The Token-level MDP for LLMs
-
Bradley-Terry preference model
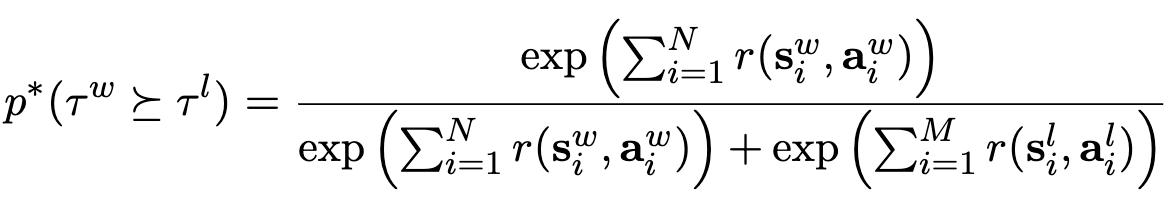
- $\bold{s}_i^w, \bold{a}_i^w$: win (preferred) state, win (preferred) action
- $\bold{s}_i^;, \bold{a}_i^;$: lose (unpreferred) state, lose (unpreferred) action
- $N$: win trajectory length
- $M$: lose trajectory length
- $p^*$: win trajectory의 reward가 loss trajectory reward에 비해 선호되는 정도 (probability)
3.2 The Classifical RLHF Methods
-
Classical RLHF Method (PPO) (Non token-level PPO == contextual bandid) (equation 2)
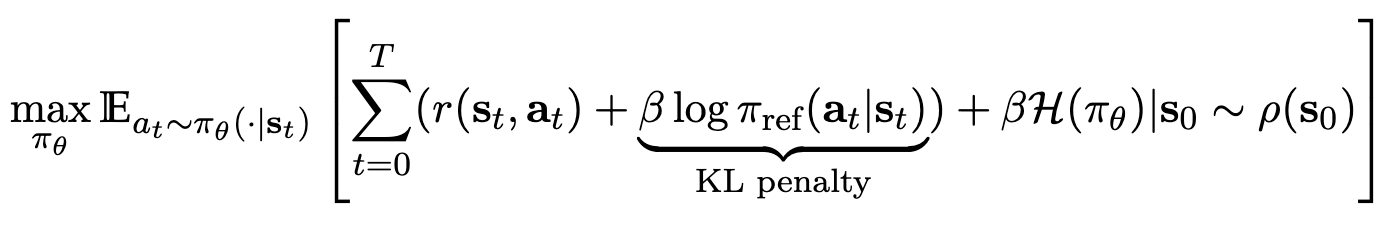
-
reward는 contextual bandid로 학습됨 $\to$ final step에서만 학습에 반영됨 ($\bold{a} == EOS$)
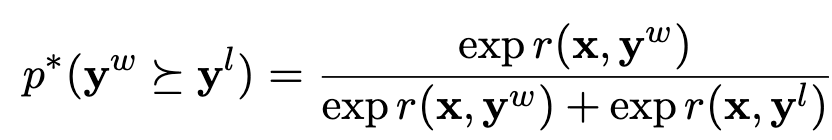
-
실제로는 Token-level PPO로 아래처럼 적용됨
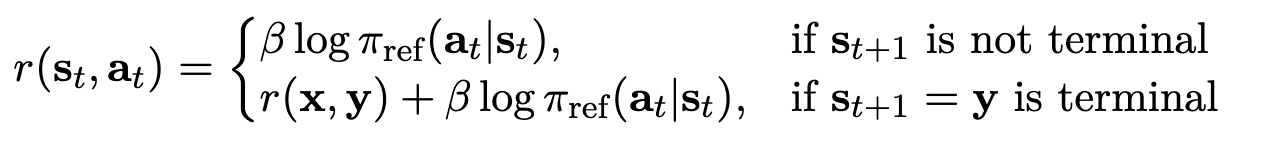
-
3.3 Direct Preference Optimization
-
PPO와 다르게 완벽한 contextual bandid setting에서 학습이됨 (Non token-level)
-
KL-contextual bandit version of RL
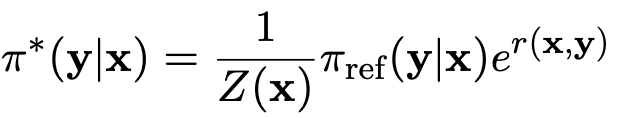
-
Reward term로 묶으면
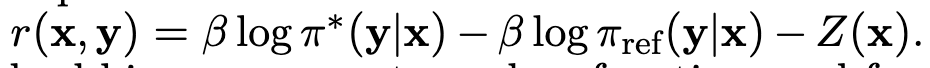
-
Preference Optimization Loss
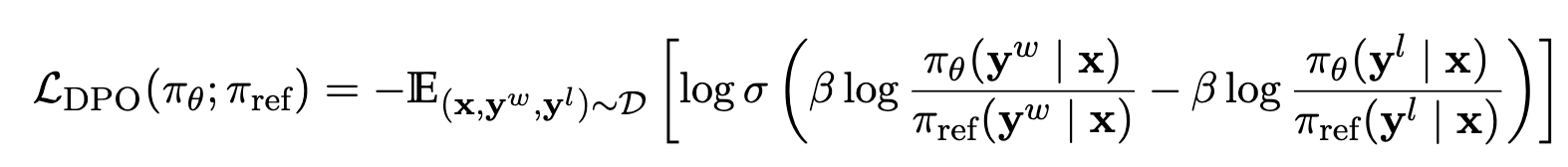
4. Theoretical Insights
4.1 DPO as a $Q$-Function in the Token Level MDP
-
Contextual Bandit 상에서 $Q$ Function
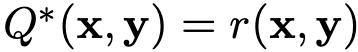
$\to$ token-level 정의가 안되므로, 새로운 정의를 제안하자
-
RL in the Token-Level MDP
-
Maximum Entrophy setting (equation 5)
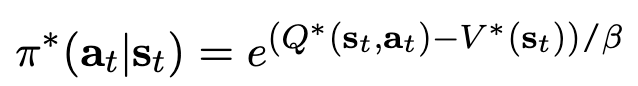
-
$Q^$: t step이후 action $\bold{a}_t$, state $\bold{s}_t$로 optimal policy $\pi^$ㅇ에 의해 기대되는 미래의 reward 총합
-
$V^$: Optimal policy $\pi^$가 모든 action들에 대해 수행하는 probability 총합
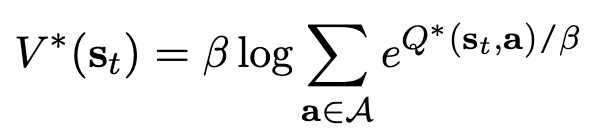
-
-
-
From $r$ to $Q^*$
-
Bellman Equation으로 구현 (재귀표현) (equation 7)
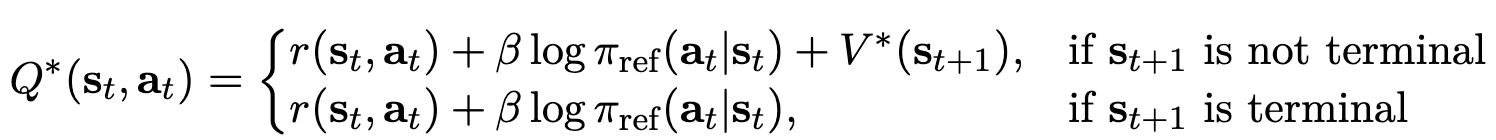
-
-
DPO가 best estimate $Q^*$를 학습함을 유도
-
위 식을 reward $r$에 대해 정리하면
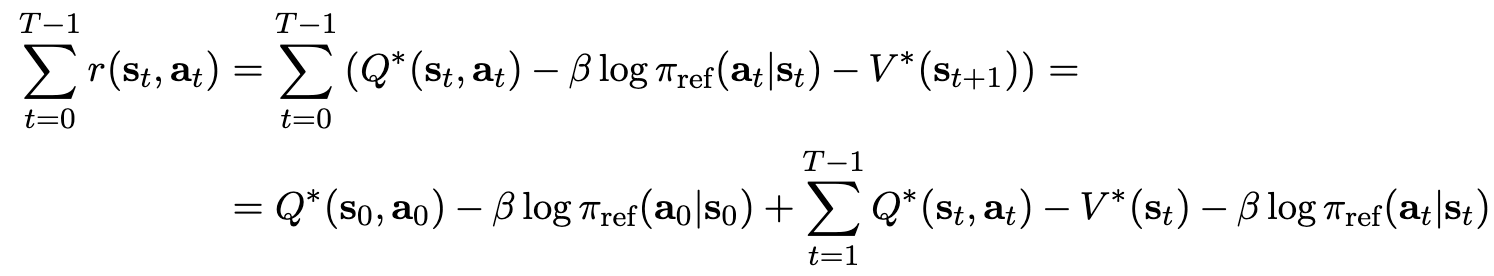
-
위 식에 $Q^* - V^$를 $\pi^$에 대해 정리하면
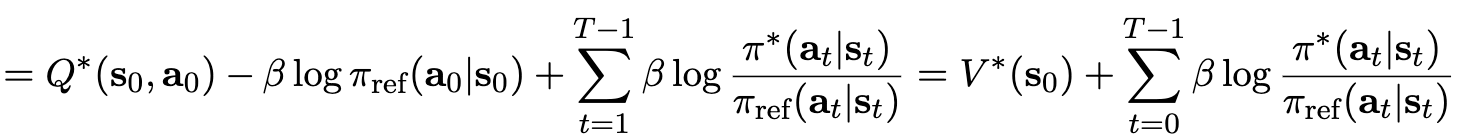
-
Preferrence indeuced model의 probability는
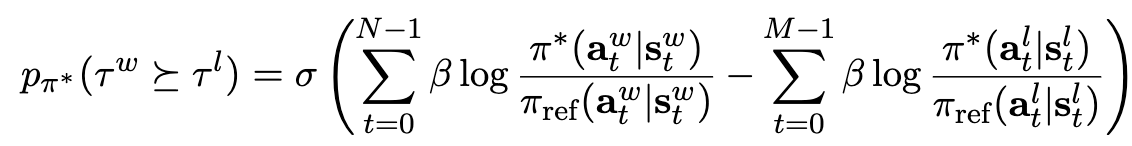
-
DPO Loss는
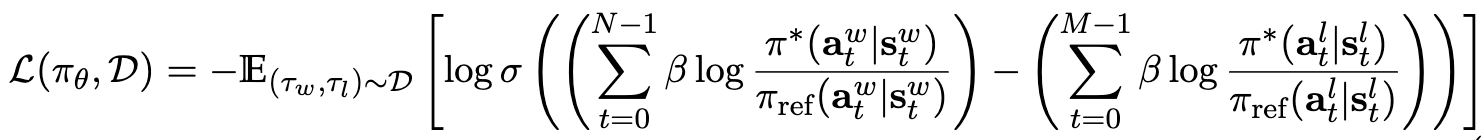
-
4.2 Token-Level DPO Can Parameterize Any Dense Reward Function
-
equation 5 & equation 7을 유도하면 (equation 10)
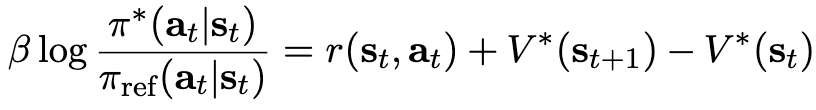
5. Practical Insights
- model: Pythia-2.8B
- dataset: Reddit
5.1 Does DPO Learn Credit Assignment?
-
질문: 고용에 관한 negotiation 상황

- Salary range와 같이 error response에 대해 reward를 잘 주는걸 확인
5.2 Connecting Guided Decoding and Search to Likelihood-Based DPO Optimization
-
LLM decoding 시 검색 기반 후처리 방식이 등장하고 있음 (Beam Search, etc)
-
Equation 7(Bellman Equation) 을 K개의 action으로 확장해보면
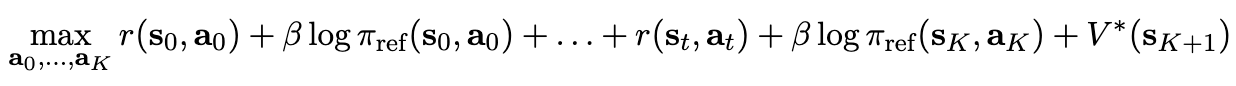
-
Equation 10을 위식에 대입하여 정리하면
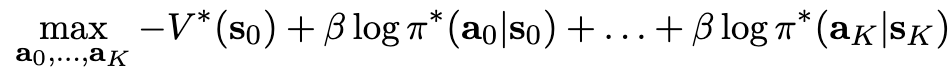
$\to$ 시작 상태는 고정되므로 ($V^(\bold{s}_0)$) optimal policy ($\pi^$) 기반 검색 알고리즘은 해당 최적 정책에 대한 likelihood 검색과 동일함
-
Beam의 갯수에 따른 성능 분석
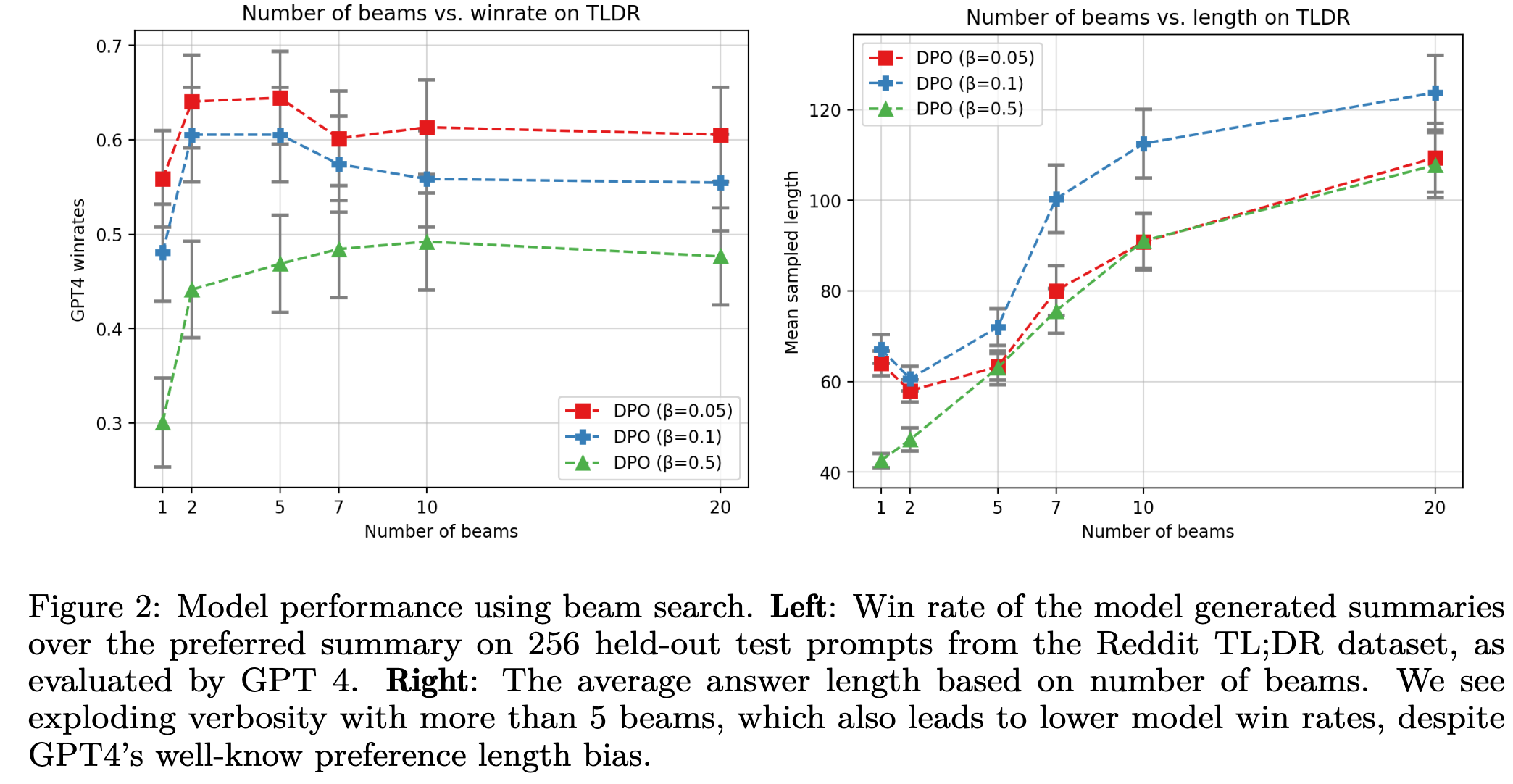
- Beam이 5개까지는 성능이 향상됨 $\to$ reward hacking을 방지하기 때문으로 사료됨
5.3 Likelihoods should decrease when using DPO
-
SFT이후 DPO를 진행하면 preferred sample에 대한 likelyhood가 증가할걸로 예상되나, 실제로는 그렇지 않음
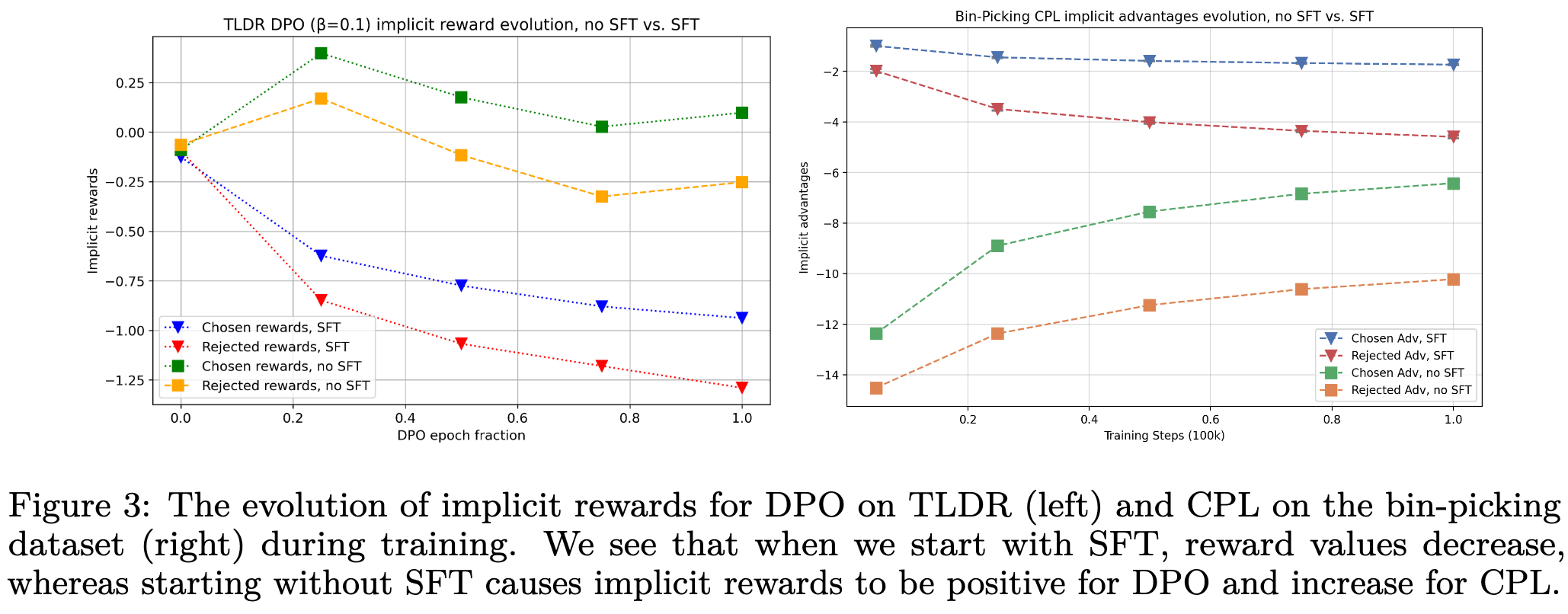
-
이는 DPO에 사용되는 KL Divergence를 유심히 보면 알게됨