[LT][CLS] Long-Tail Learning via Logit Adjustment
[LT][CLS] Long-Tail Learning via Logit Adjustment
- paper: https://arxiv.org/pdf/2007.07314.pdf
- github: https://github.com/google-research/google-research/tree/master/logit_adjustment
- ICLR 2021 accepted (인용수: 456회, ‘23.12.06 기준)
1. Motivation
-
Long-tailed classification 문제를 푸는데 domiant label에 biased된 학습을 하곤 한다.
-
기존에 LT문제를 풀기 위해 사용되는 label adjustment 기반의 방법론을 검토한다.
-
weight normalization : optimizer에 따라 성능 차이가 발생함
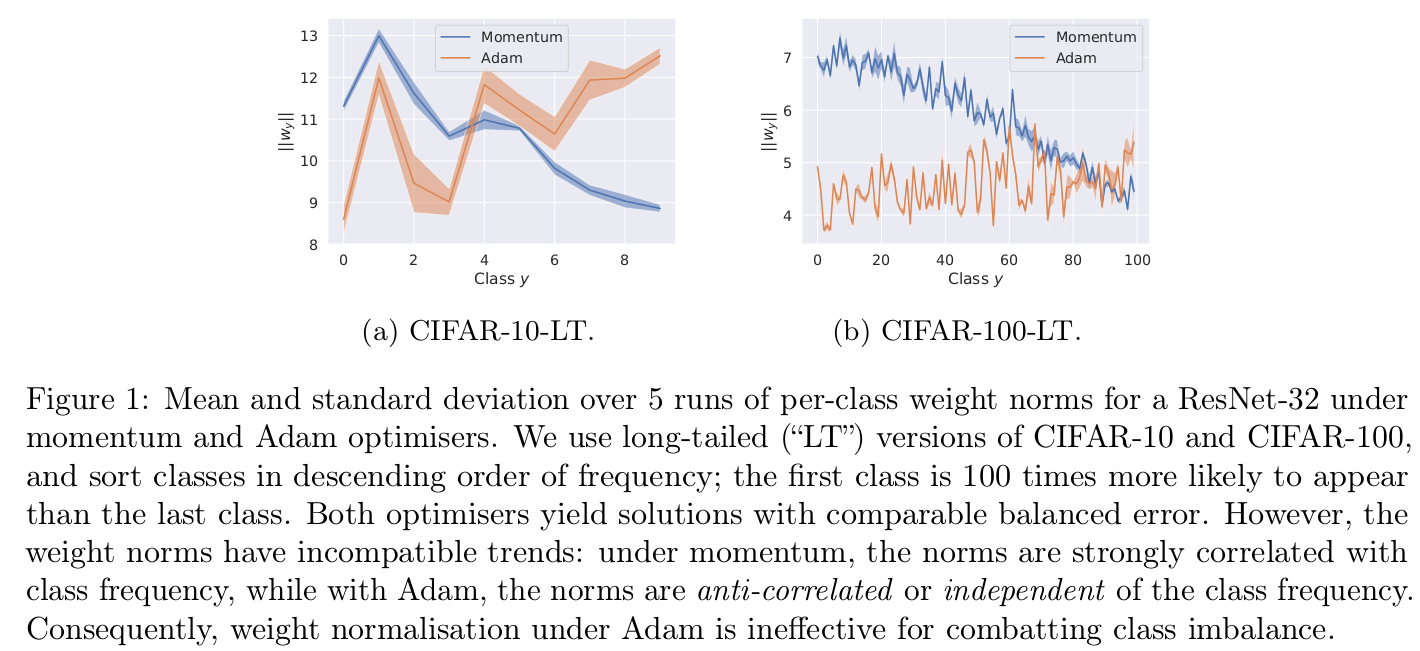
- SGD optimizer : weight norm값과 class frequency 패턴이 유사함 (class 0 -> 100 갈수록 적어지는 데이터 CiFAR-100-LT)
- Adam optimizer : 다른 경항
-
loss modification : argmax를 취했을 때, consistency 문제가 발생함
-
Fish Consistency : Balanced error를 최소화하는 결과와 loss modification으로 인한 error를 최소화 하는 결과가 같아야 한다
-
Balanced Error : Imbalance classification에서 주로 사용하는 Loss (or Metric)
가령, native
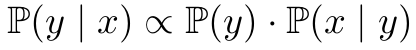dominant class로만 예측하면 accuracy가 증가하는 문제가 있음하지만,
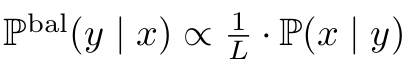는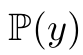 
에 dependent하지 않음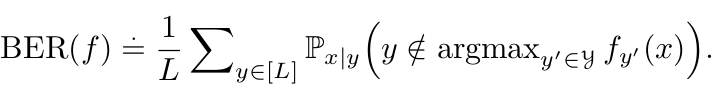
- $L$: Number of class
- $y$: label
- $x$: image
- $y’$ : negative label
-
기존 방식은 positive $y$의 frequency와 negative $y’$의 frequency를 모두 고려하고 있지 않음
-
하지만 본 논문에서는 통계적 background를 바탕으로 fisher consistent margin을 부여함
-
-
-
2. Contribution
- Long-Tailed problem에 적합한 logit adjustment을 기반으로 하는 두 가지 방법론을 제안함
- post-hoc : 학습 없이 post-hoc으로 진행
- during training (softmax loss기반) : 학습 병행하여 추가 성능 향상
- pairwise label margin을 추가한 General한 Softmax version의 loss를 제시
- 기존 방식들의 한계인 Balanced Error에 대해 Fisher consistent하지 못하다는 문제를 해결함
- Real-world dataset에서 성능 향상이 있음을 보임
3. Problem setup
-
Softmax Cross Entropy Loss
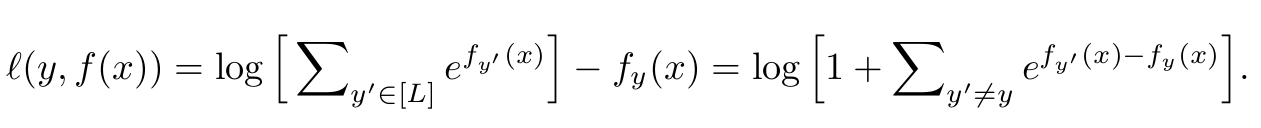
- $f(x)$: model의 softmax 통과 전 output
- $L$: number of Class
-
Previous Methods
-
input을 건드림 : over-sampling / under-sampling
-
output을 건드림 : pos-hoc correction
-
internal 값을 건드림 : loss 함수 변경, 등
여기서는 output / internal 두 방식을 중점으로 재점화
-
3.1 Post-hoc
-
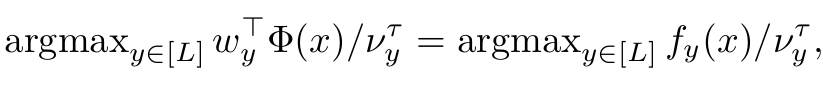
$\nu_y$: weight term for label $y$. could be weight 2-norm or label y’s distribution
-
$\Phi(x)$: feature before classification weight of input $x$
-
$w_y$: classification weight for label $y$
단점: weight norm의 경우, optimizer dependant함. 그렇다고 $\nu_y=\pi_y$ 즉 label $y$의 분포를 direct하게 쓴다 해도 label ordering이 달라지는 이슈가 생김
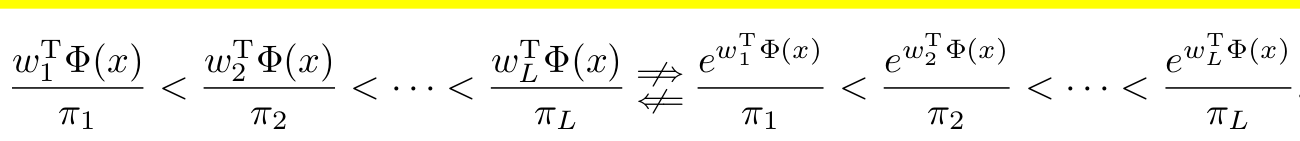
3.2 Loss modification
- 다양한 형태의 Loss modification이 있음
-
Balance loss
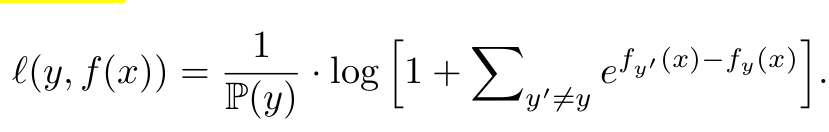
- label $y$ 의 prediciton score의 역수를 곱해 imbalance한 class에 대한 가중치를 높임 -> decision boundary를 dominant class쪽으로 밀어내는 역할
-
Hingle loss
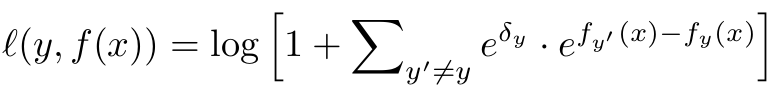
- class label마다 per-class margin $e^{\delta_y}$를 곱한 형태. $ \propto \mathbb{P}(y)^{-1/4}$
- rare positive $y$와 any negative $y’$간의 더욱 큰 margin을 부여
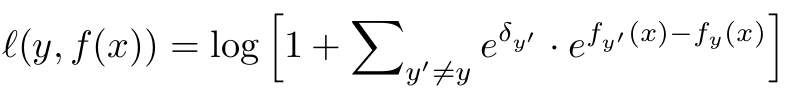
- $\delta_{y’} \leq 0$: non-decreasing transform.
- 직관적으로 negative dominant label $y’$에 대해 음의 margin을 주어, rare positive $y$에 대해 gradient가 inhibit되는 것을 방지
단점: 모든 기존의 Loss modification들은 either $y$ 혹은 $y’$의 분포만 고려했지, 둘 다 고려하고 있지 않음 -> fisher consistency가 무너짐
4. Logit Adjustment for long-tailed learning : Statistical Review
-
목표: Balanced error를 최소화
-
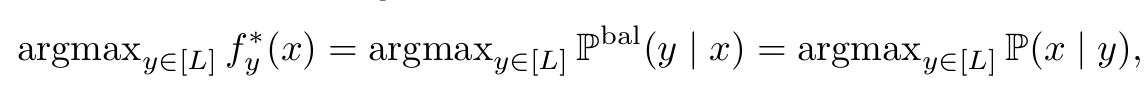
위 식에서 $\mathbb{P}^{bal}(y x) \propto \frac{1}{L} \mathbb{P}(x y)$이기 때문에 2, 3번째 equal 이 성립함 (L은 상수) -
정의에 의해 $\mathbb{P}^{bal}(y x) \propto \mathbb{P}(y x)/P(y)$ 임 -
$\mathbb{P}(y x) \propto e(s^_y(x))$, $s^: x \to \mathbb{R}^L$ 인 scorer이므로
-
-
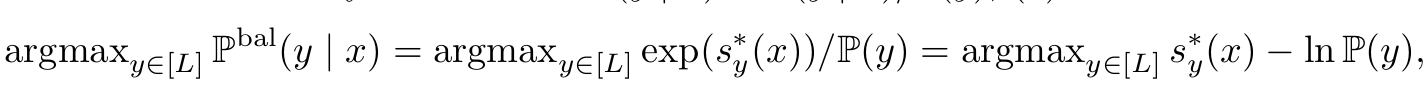
위 식을 optimize하기 위한 두 가지 방법
- Post-hoc: 기존의 standard
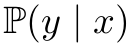를 학습시키고, class prior y의 분포에 대한 log값을 빼준다. - Train:
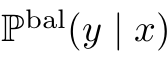을 위 식처럼 수정해서 학습한다.
5. Post-hoc Adjustment
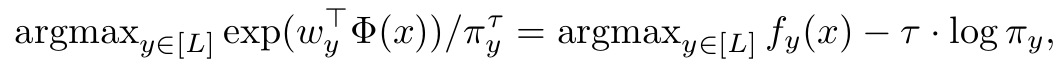
- $\tau >0$: hyperparameter. 1이면 위 4장에서 다룬 balanced error 와 동일. 아니면 temperature scaling한 post-hoc
- $\pi_y$: true label $y$의 distribution
6. The Logit Adjusted softmax cross-entropy
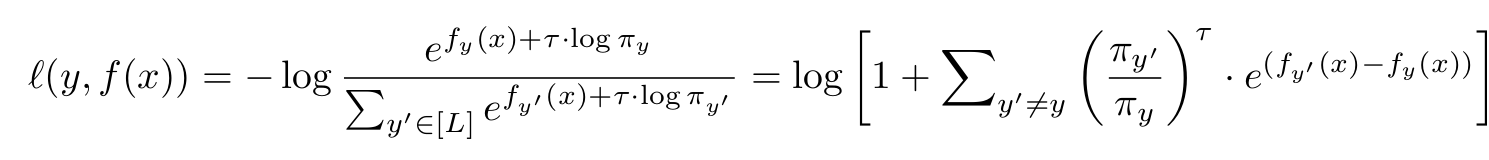
- $\pi_{y’}$: label $y’$의 distibution 분포
- $\pi_{y}$: label $y$의 distibution 분포
- $f_{y’}$: label $y’$의 softmax 이전 model output feature
-
$f_{y}$: label $y$의 softmax 이전 model output feature
-
위 식은 scorer $g_y(x)=f_y(x)+\tau log(\pi_y)$를 학습시키고, pos-hoc adjustment처럼 $\tau log(\pi_y)$를 logit에 추가한 형태로 볼 수 있음
-
이를 일반화 하면
-
$\Delta_{yy’}$: desired label margins between $y$, $y’$
ex.
- $\alpha_y=1$ , $\Delta_{yy’}=log(\frac{\pi_{y’}}{\pi_y})$ 면 6장의 adjusted softmax cross-entropy
- $\alpha_y=\frac{1}{\pi_y}$ , $\Delta_{yy’}=0$ 면 3.2장의 balanced loss
- $\alpha_y=1$ , $\Delta_{yy’}=\pi_y^{-1/4}$ 면 3.2장의 hinge loss
-
-
Theorem 1
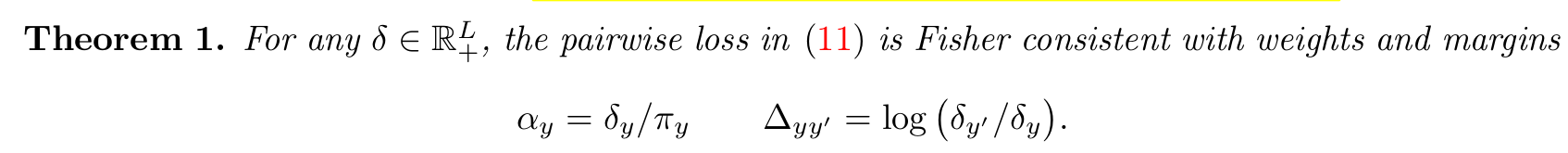
- $\delta_y=\pi_y$면 logit adjusted softmax cross-entropy 가됨