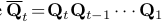[DM][LG] LayoutDM: Discrete Diffusion Model for Controllable Layout Generation
[DM][LG] LayoutDM: Discrete Diffusion Model for Controllable Layout Generation
- paper: https://arxiv.org/pdf/2303.08137
- github: https://github.com/CyberAgentAILab/layout-dm
- CVPR 2023 accepted (인용수: 44회, 2024-05-17 기준)
- downstrema task: Layout Generation
1. Motivation
-
Diffusion이 image뿐만 아니라 text generation에도 좋은 성능을 보이고 있음
-
특히 discretized space는 text 생성 시 잘되고 있음 (D3PM)
$\to$ Discretized space에서 layout을 generation해보면 어떨까?
2. Contribution
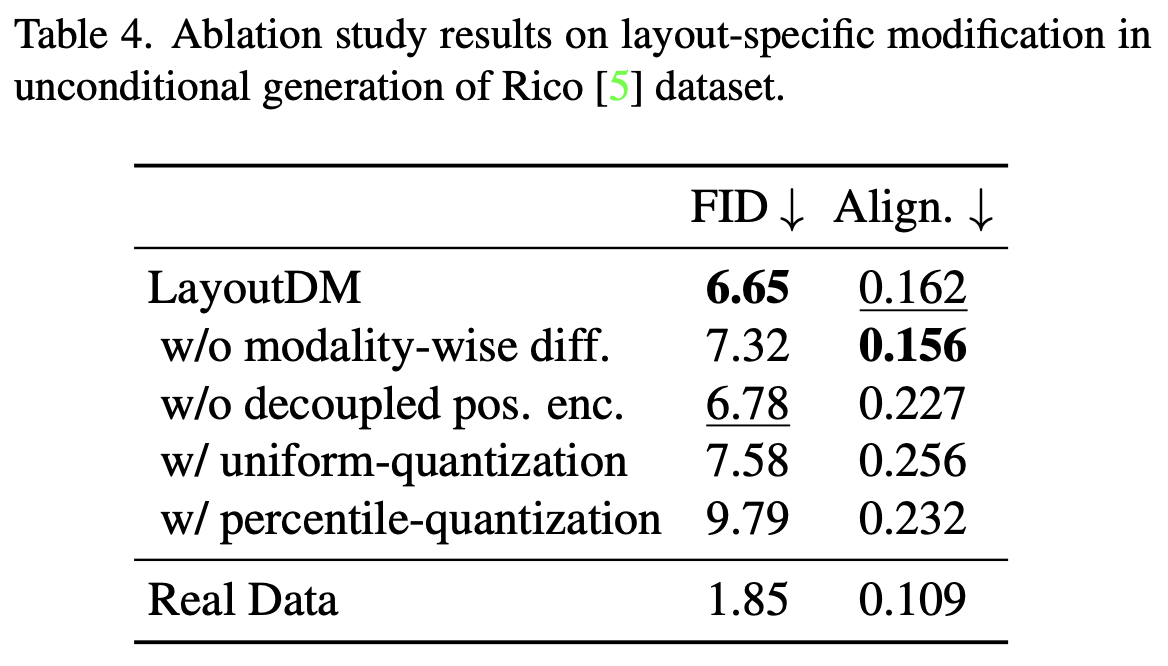
- Discrete diffusion process를 Layout generation task에 적용하기 위해 modality-wise diffusion을 제안하고, dynamic layout size를 고려한 padding approach를 적용함
- modality-wise diffusion: entity (class), x, y, w, h 등 modality마다 transition matrix를 denosing step별로 구분해서 denoising
- padding approach: Max layout 갯수를 predefined하고 document별로 layout을 할당하고 남은 tokeN에 대해 [PAD] token으로 setting
- Inference때 [Masking] token과 logit adjustment를 사용한 layout constraint를 적용하여 single model로 multi-task (C$\to$S+P, C+S$\to$P, completing, refinement, 등) 수행 가능해짐
- 다양한 layout generation benchmark에서 준수한 성능을 냄
3. LayoutDM
-
Preliminaries:
-
D3PM
- categorical variable을 text 생성에 맞춰 디자인한 논문
- forward process
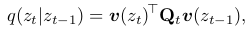
-
T: total time step
-
-
Q$_t$: transition matrix $\in [0,1]^{K \times K}$
-
[Q$t$]${mn}$ = q($z_t=m z_{t-1}=n$)
-
-
Markov property를 이용해 다음을 유도할 수 있음
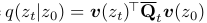
-
overall loss
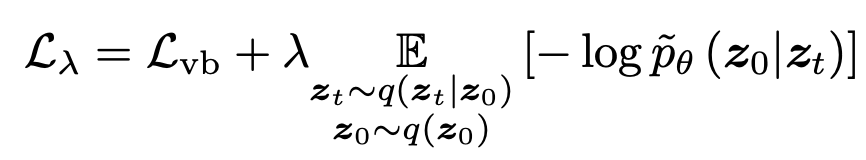
-
-
VQDiffusion : Mask-and-Replace를 통해 여러 task를 통합
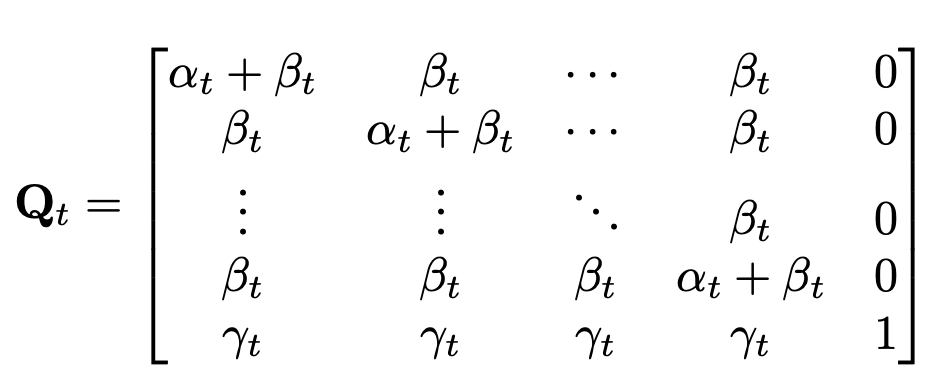
- $\alpha_t$: 기존 token을 그대로 사용하는 비율
- $\beta_t$: 다른 random token과 replace하는 비율
- $\gamma_t$: 기존 token을 [MASK] token으로 replace하는 비율
- $\in \mathbb{R}^{(K+1) \times (K+1)}$
overall diagram
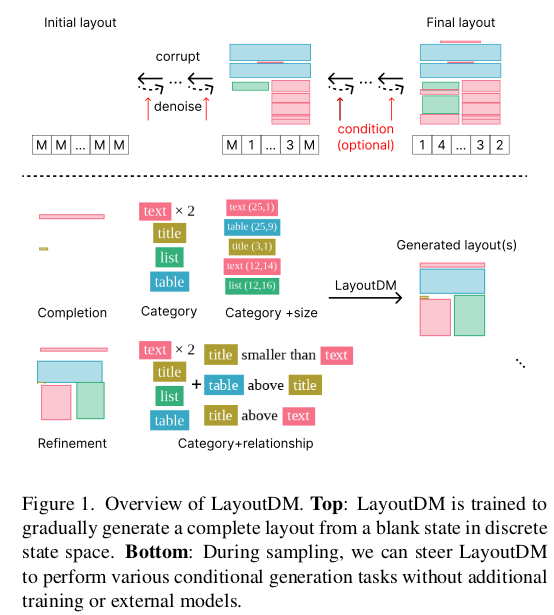
-
Unconditional Layout Generation
-
$l={(c_1, b_1), …, (c_l, b_l)}$
-
b_1은 0~1로 normalized된 bbox로, discretized bin 수행
-
Noise는 각 modality별로 아래와 같이 줌
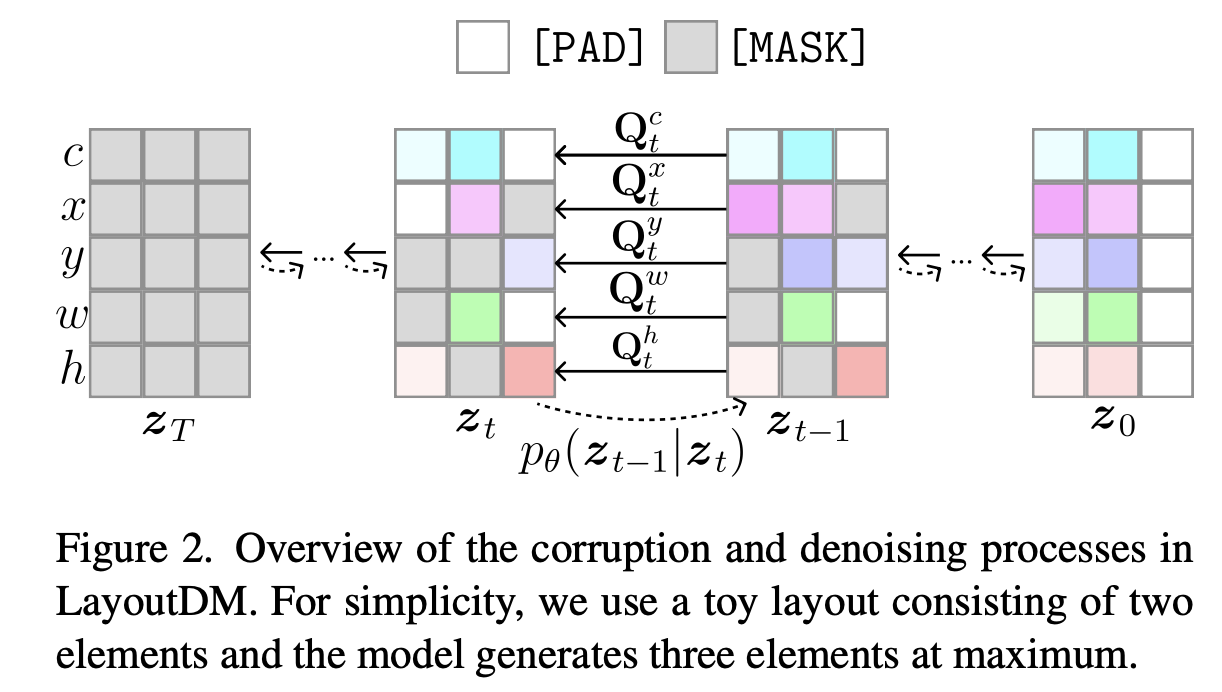
-
Variable Length Generation
-
class 갯수 K + 2 (mask token, padding token)
- Modality-wise Diffusion
- $Q_t^c \in \mathbb{R}^{(K+2) \times (K+2)}$
- 나머지는 $Q_t \in \mathbb{R}^{(B+2) \times (B+2)}$
- Adaptive Quatization
- 각 modality별로 분포가 다르므로 uniform quantization보다 K-means quantization 수행하는게 효과적임
-
-
Decoupled Positional Encoding
- 기존 연구들은 1-D flatten layout sequence에 positional encoding을 embedding하였음
- 반면, 여기서는 i, j decoupled시켜 positional encoding을 수행했음. $\to$ 실험적으로 성능이 좋아짐
- 기존 연구들은 1-D flatten layout sequence에 positional encoding을 embedding하였음
-
-
Conditional Generation
-
Strong Constraint : masking처리된 token에 대해서만 모델이 예측한 값으로 복원하고, 나머지는 gt 그대로 활용
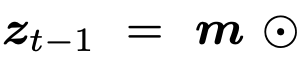
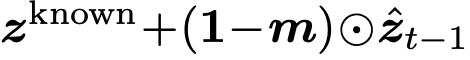
-
Weak Constraint: Logit adjustment를 통해 별도의 network 없이 Unified model로 target condition을 생성하도록 유도
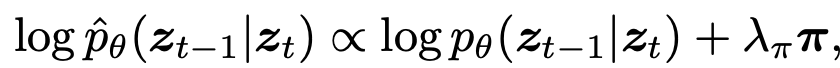
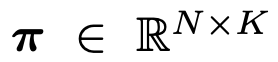 : desired term이 생성되도록 유도하는 prior weight term
: desired term이 생성되도록 유도하는 prior weight term- $\lambda_{\phi}$: hyper-parameter
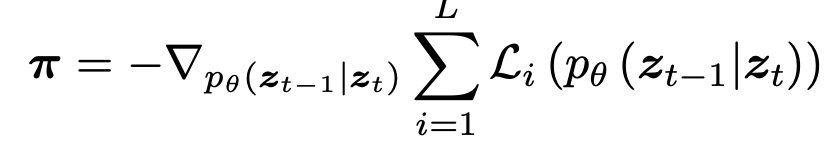
-
4. Experiments
-
Quantitative Result on Conditional Generation
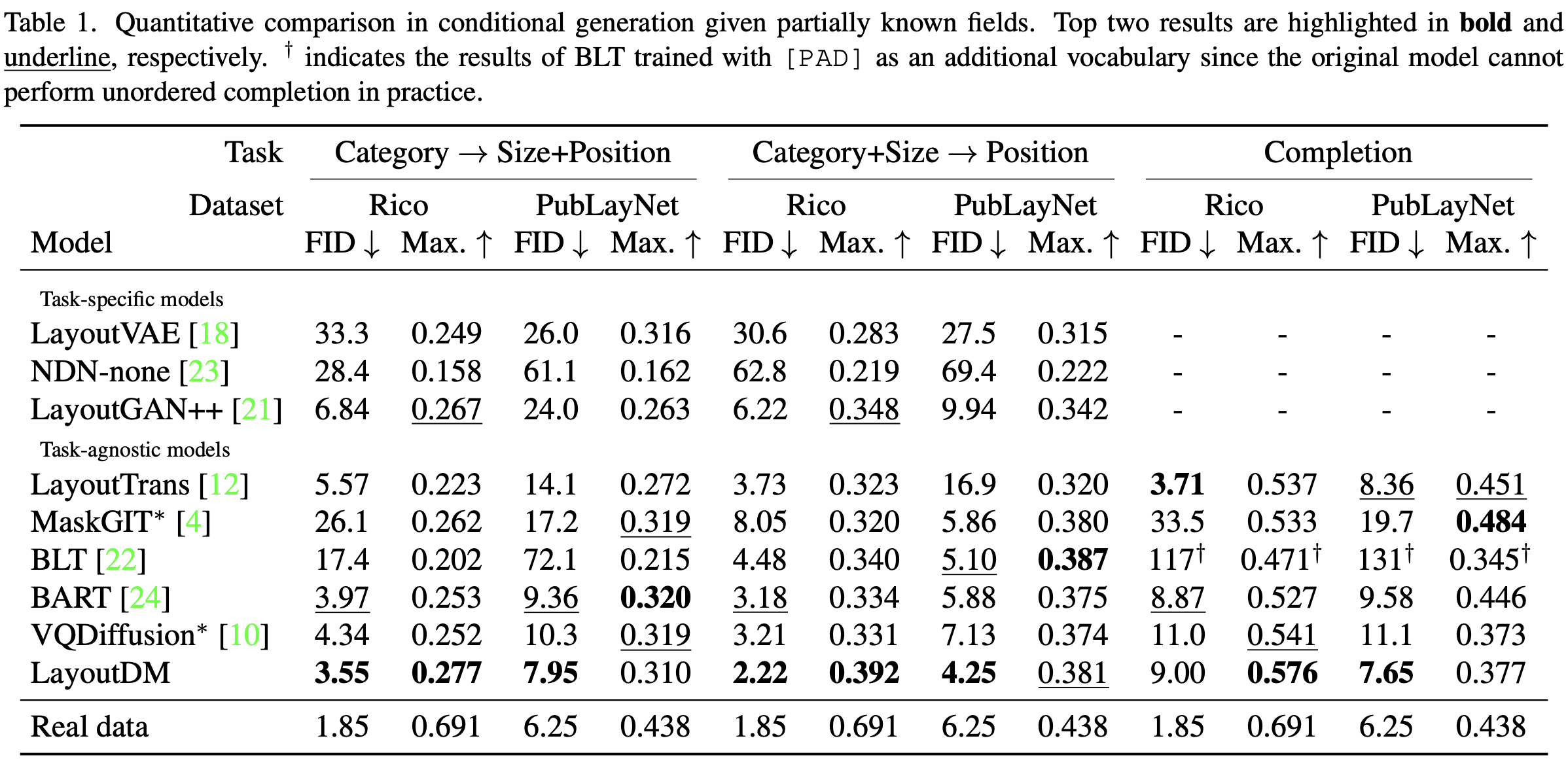
-
Qualitative Result on Conditional Generation
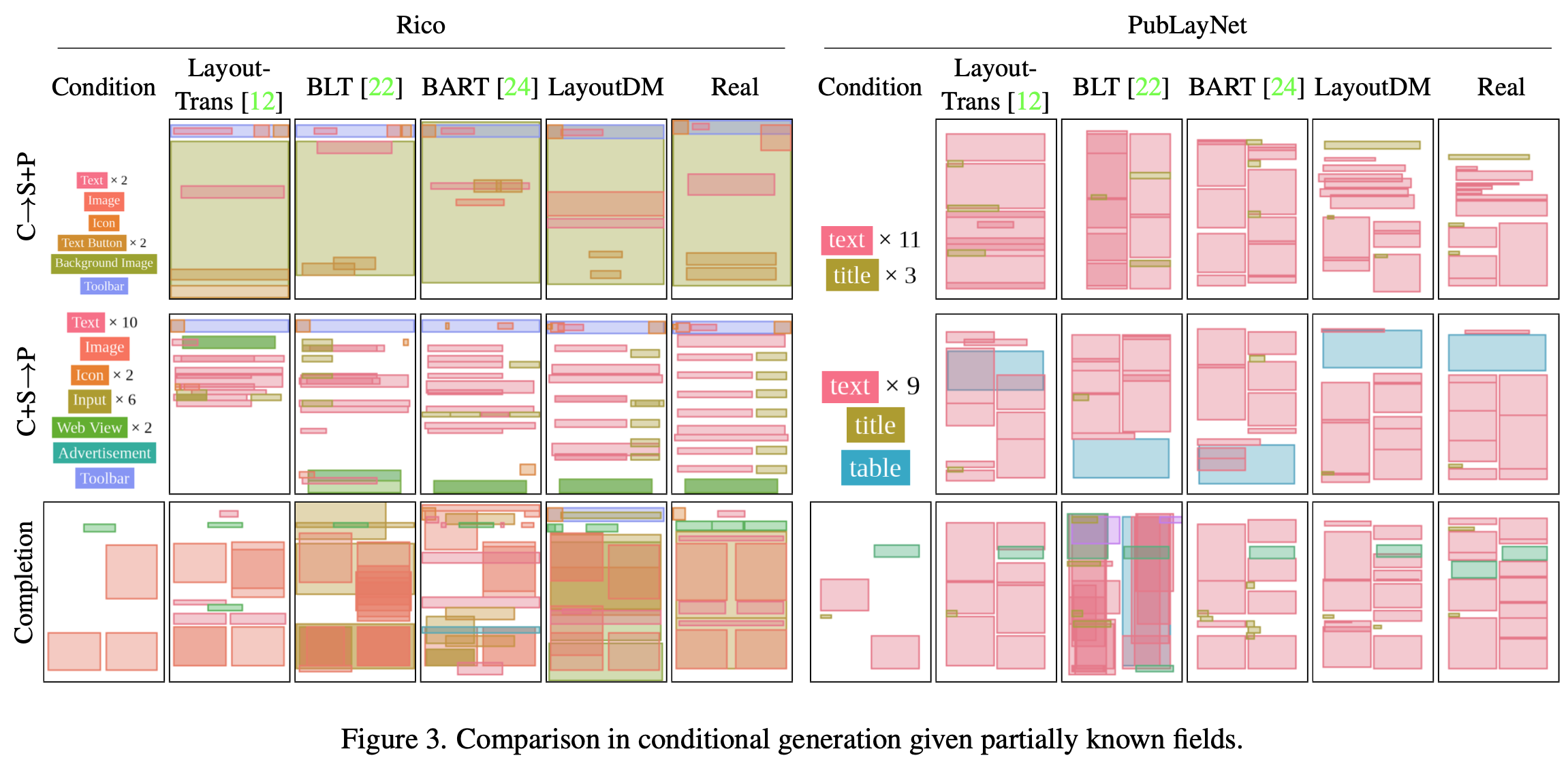
-
Quantitative Result on Unconditional Generation
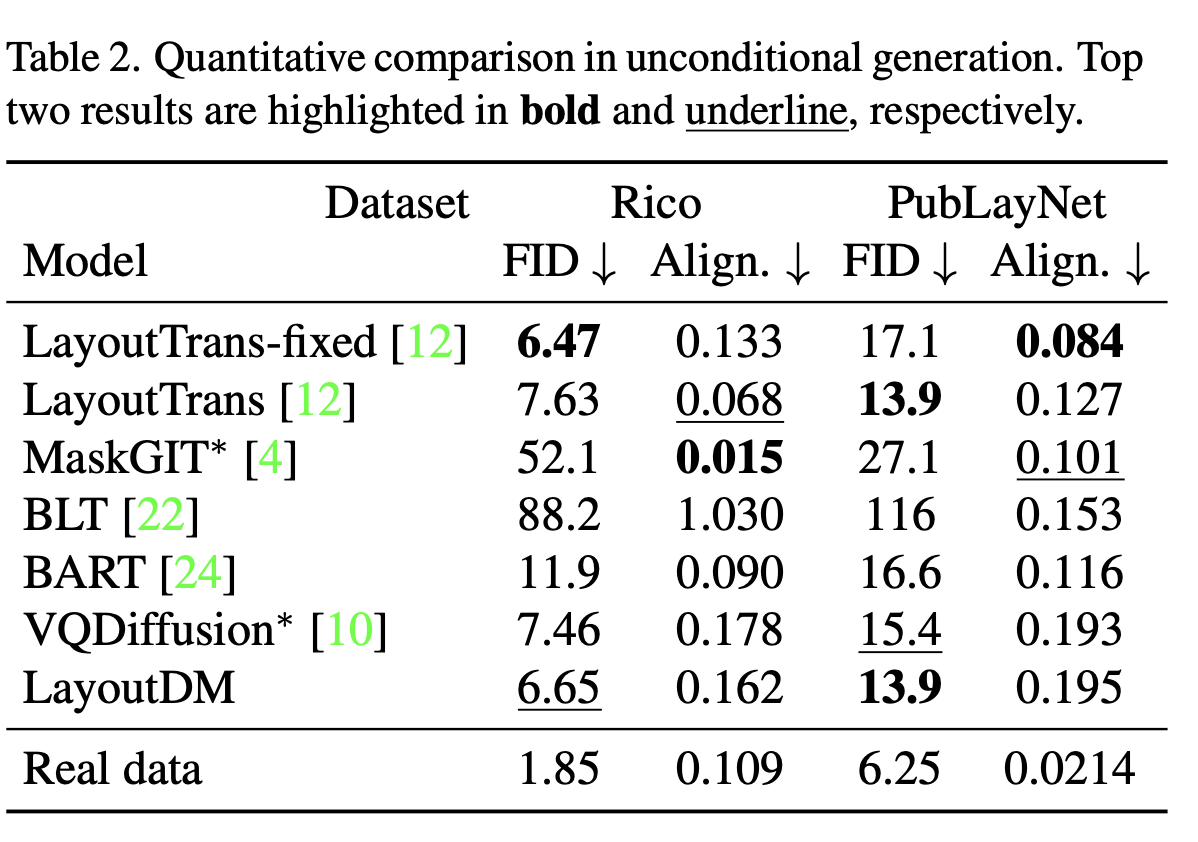
-
Quantitative Result on refinement task
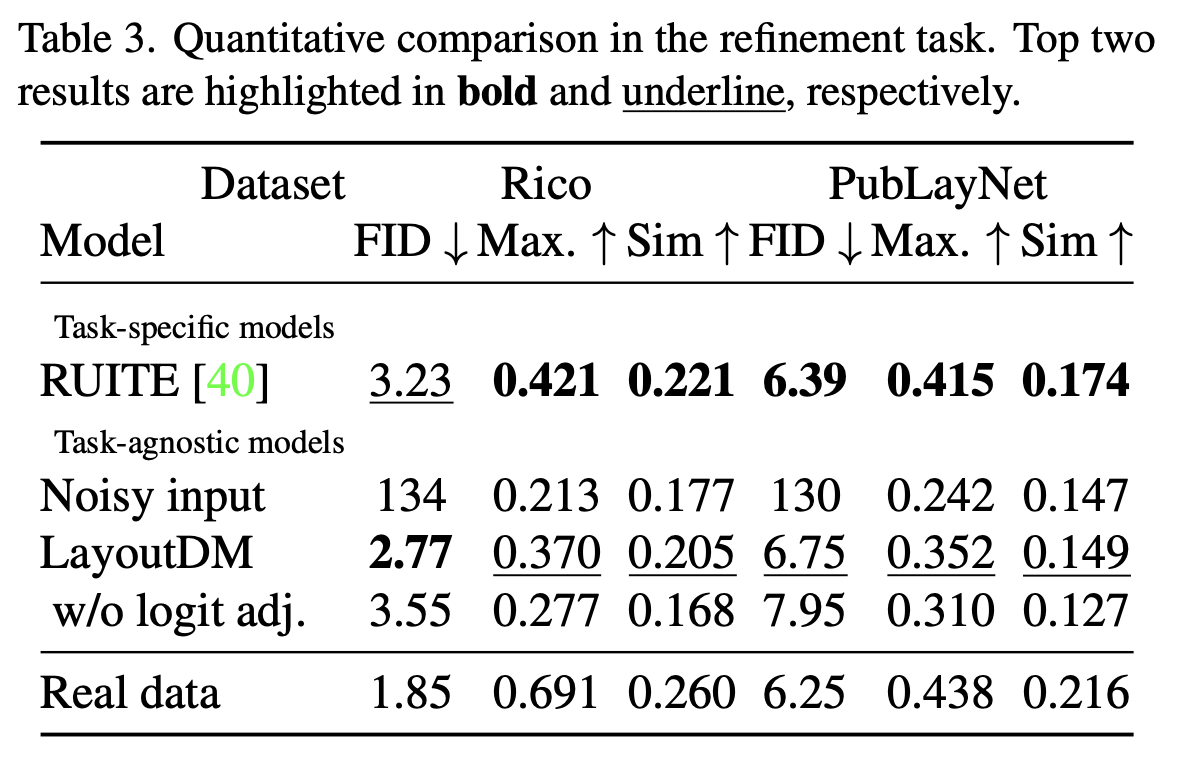
-
Qualitative Result on refinement task
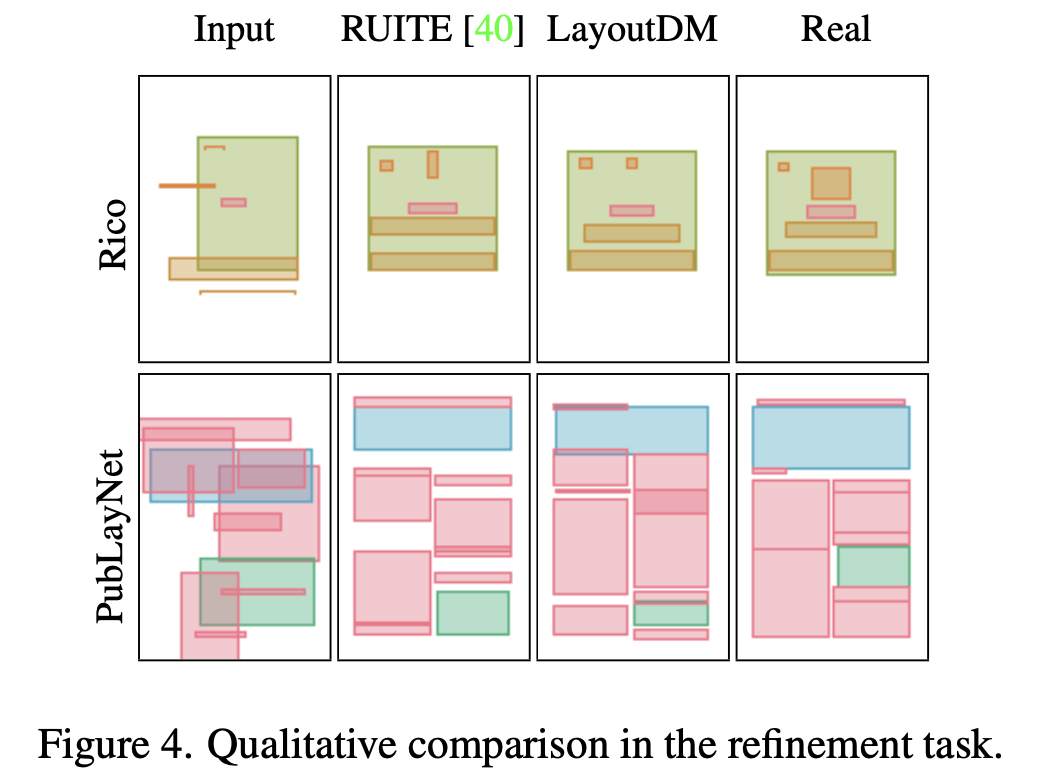
-
Quality vs. Violation trade-off
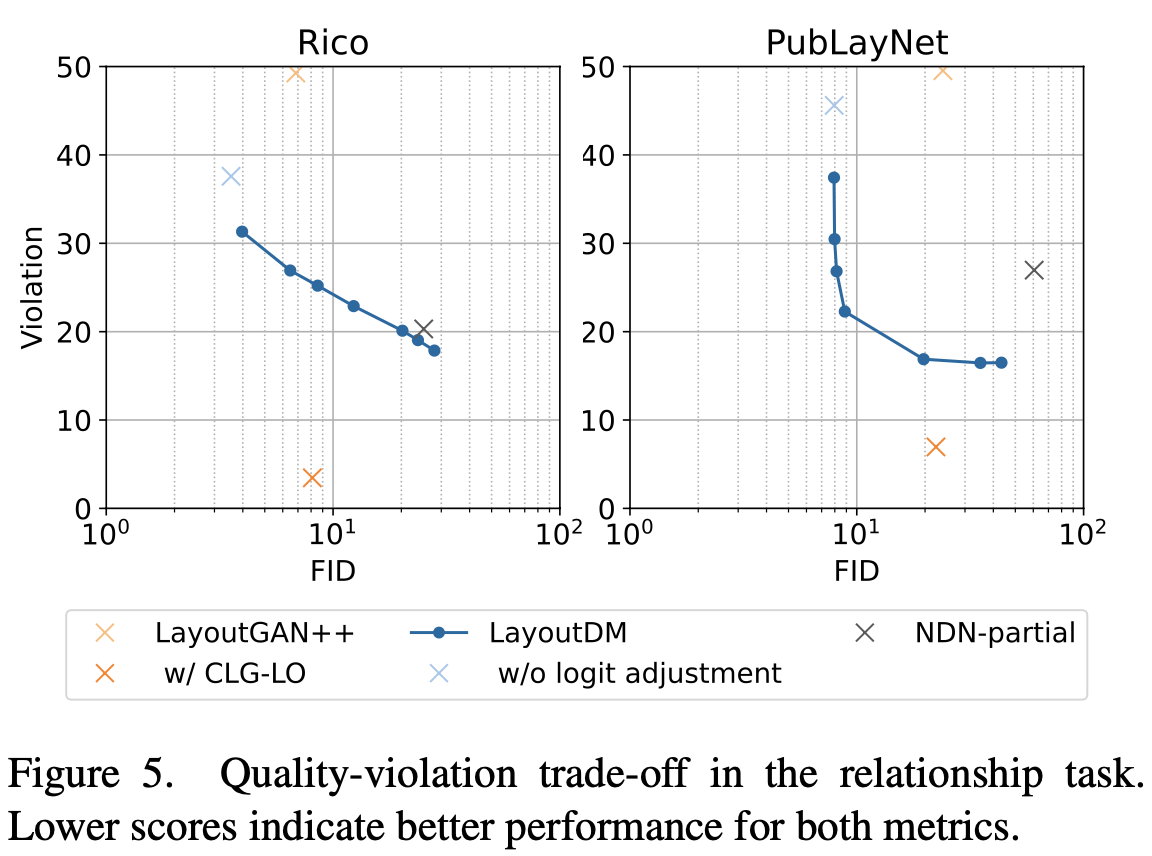
-
Relation task
-
Definition
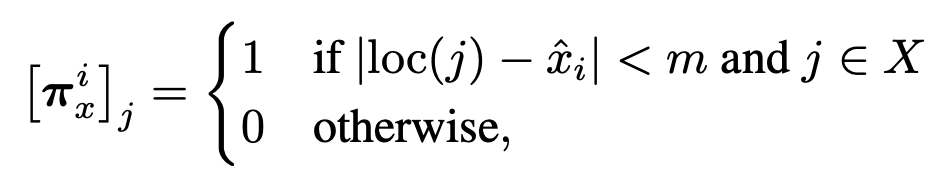
-
Result
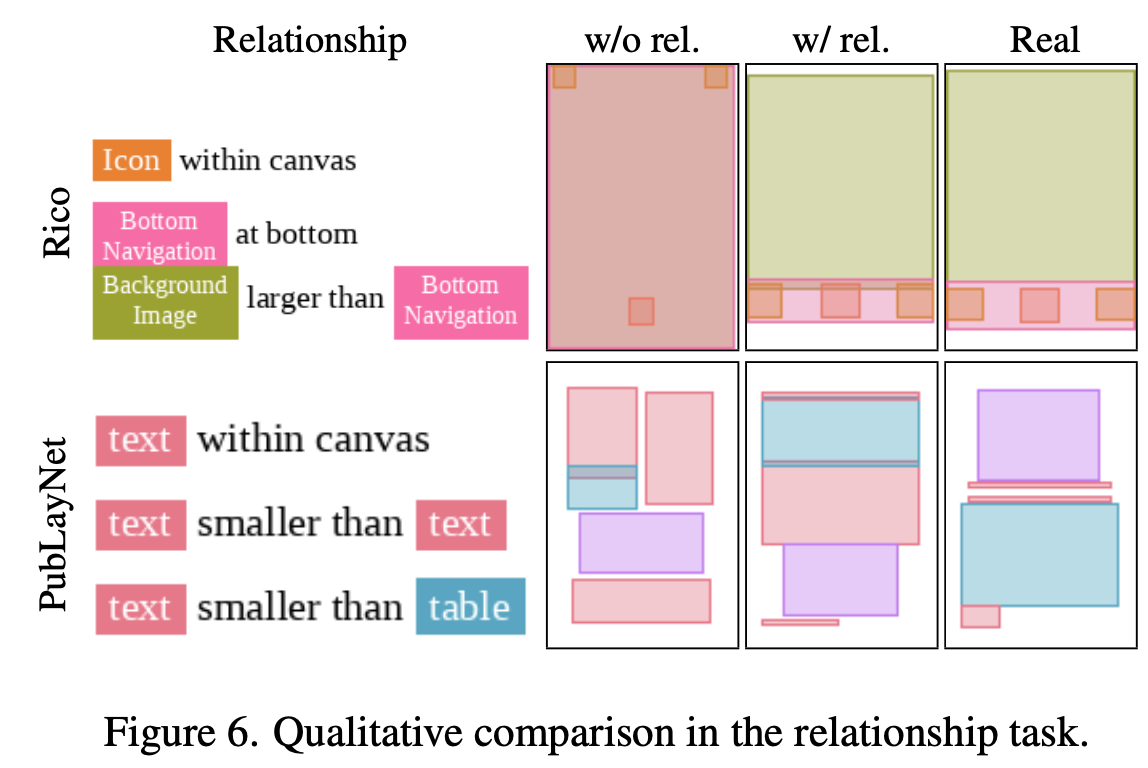
-
-
Speed vs. Quality trade-off
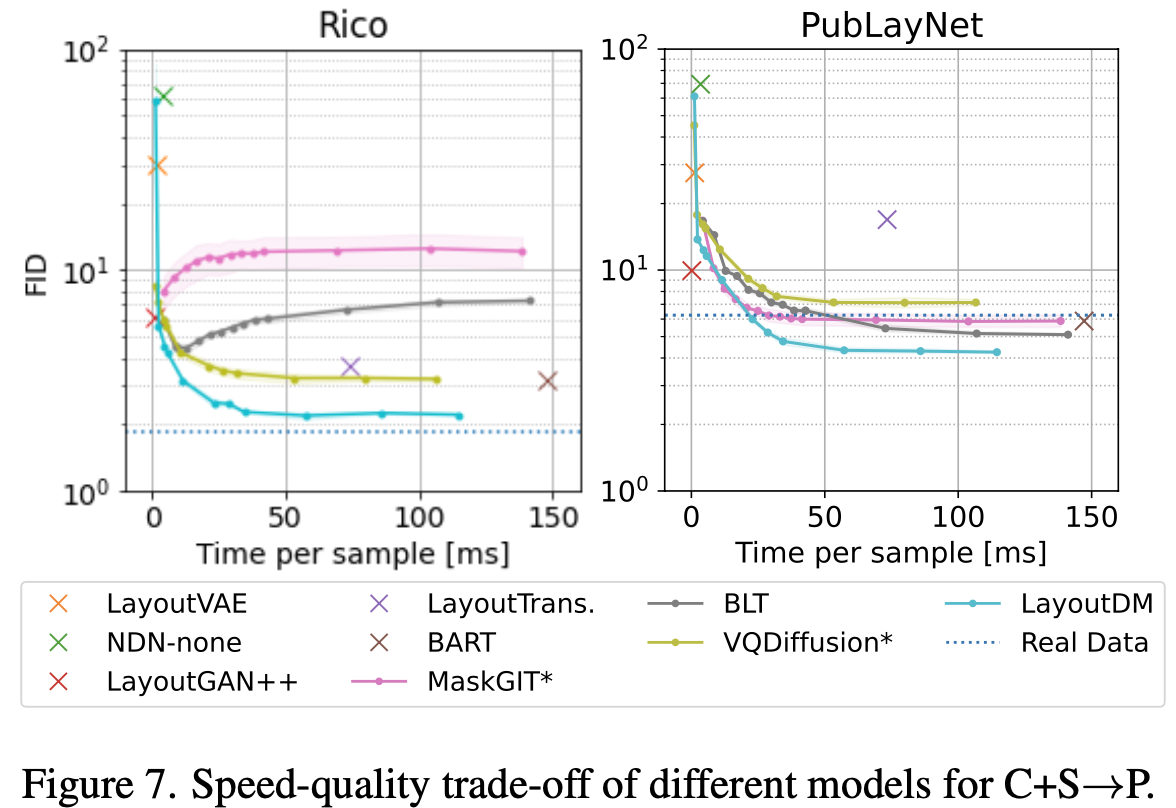
-
Ablation study