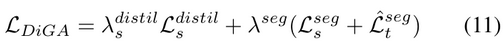[CDA][SS] DiGA: Distil to Generalize and then Adapt for Domain Adaptive Semantic Segmentation

[CDA][SS] DiGA: Distil to Generalize and then Adapt for Domain Adaptive Semantic Segmentation

• paper : https://arxiv.org/abs/2307.15063

• git: https://github.com/fy-vision/DiGA

• CVPR 2023 (‘23.09.12 인용수 1회)

• downstream task : UDA for semantic segmentation

• Contribution

  • warm-up stage:

    

    • Supervised learning뿐 아니라 feature-alignment loss를 teacher-student network끼리 주어 augmentation에 대해 robust한 generalizability를 확보
    • Cross-Domain-Mixture (CrDoMix) data augmentation을 주어 성능 향상

  • self-training stage:

    • Bilateral-consensus pseudo-supervision으로 threshold-free self-training 기법을 제안
      • feature-induced labels (pixel-to-centroids)
      • probability based labels (from warm-up model)

• Warm-up stage

  • Supervised Loss → 기존 CE 와 동일

  • Distillation Loss : Class 정보를 알고 있는 source dataset에 대해

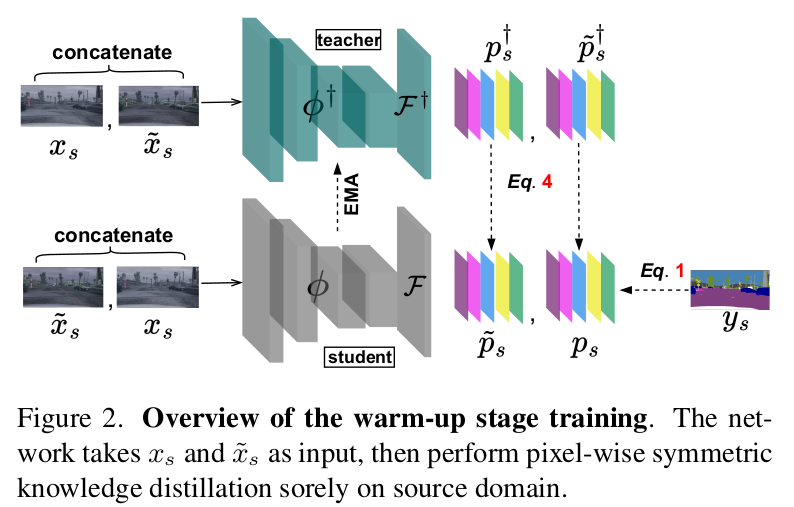
    • teacher 한테 weak augmentation / student한테 strong augmentation을 주어 symmetric KD Loss를 줌

      

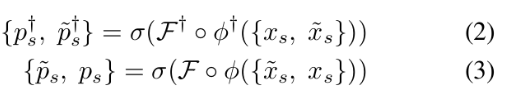
      • $F^+, \phi^+$ : teacher의 encoder, teacher의 segmentation head
        • teacher는 Ema update
      • $F, \phi$ : student의 encoder, student의 segmentation head

    • fine-grained label에 의한 ovefitting 방지 목적으로 soft-label 사용

      

  • Cross-Domain-Mixture augmentation (CrDoMix)

    

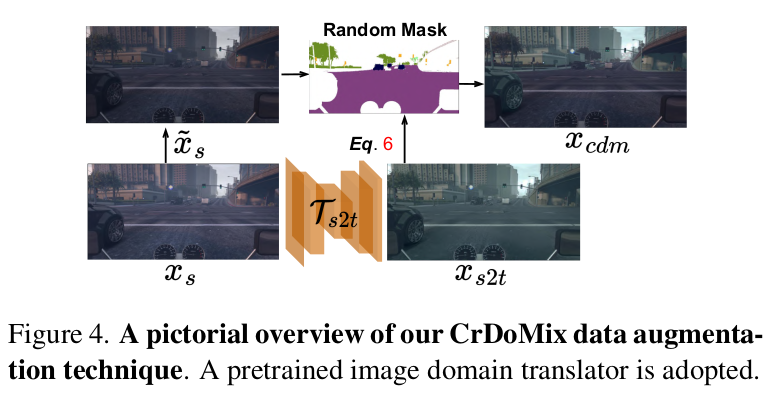
    • Pretrained, Fixed Cycle GAN (Source 2 Target)을 활용!

    • binary mask를 사용하여 mixture

      

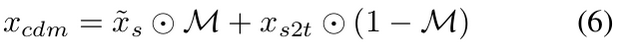
      • source data의 기하학적 모양을 헤치지 않음 → No label change!
      • 추가 batch 늘릴 필요가 없음
      • Target domain 정보를 흘려주며 학습 가능!

• Threshold-free Self-Training

  

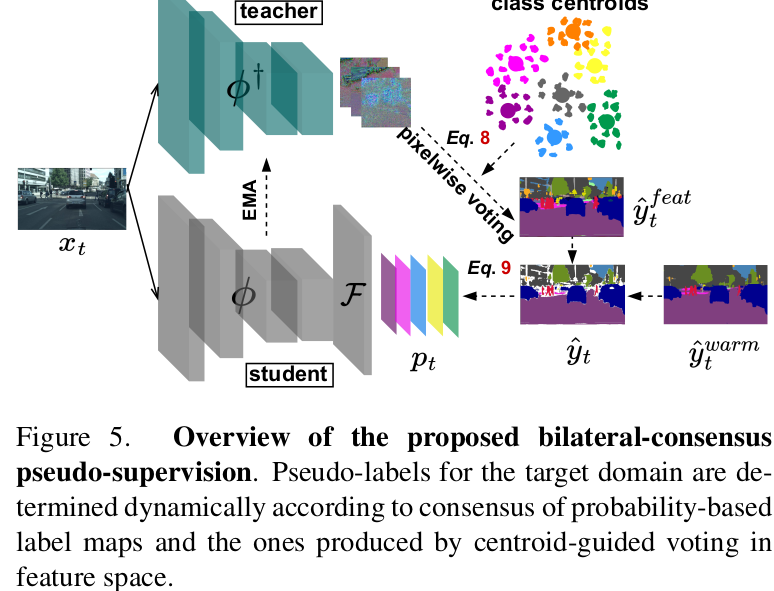
• Centroids

  

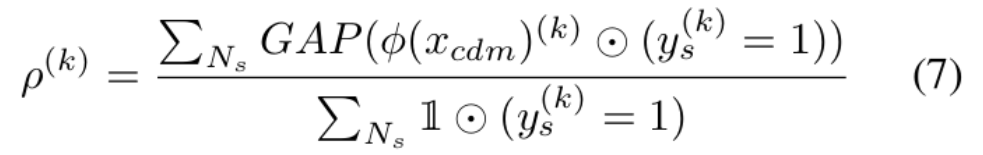
  • GAP: Global Average Pooling
  • $x_{cdm}$ : 6번식 결과
  • $\phi$ : warmup Model의 feature
  • $\rho^k$ : k class의 centroid
  • Warm-up Model을 활용해서 Class centroid를 추출함 → Noise label voting 시에 활용할 목적
  • initial value : warmup model의 class-wise feature

• Feature-induced labels

  

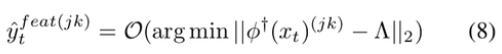
  • centroid와 teacher feature 간의 제일 similar한 class로 jk pixel을 label → local structure

• Probability-based labels

  • pseudo-supervision based on Warmup Model prediction → global structure

• Pseudo-supervison Loss

  

  

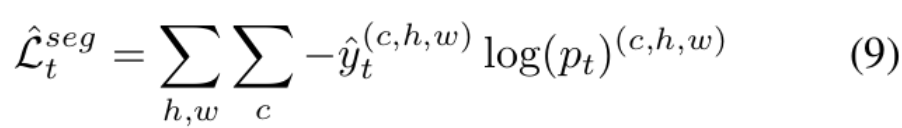
  • $p_t$: student prediction

• Full objective