WebRL: Training LLM Web Agents Via Self-Evolving Online Curriculum Reinforcement Learning

6 minute read

[WebAgent] WebRL: Training LLM Web Agents Via Self-Evolving Online Curriculum Reinforcement Learning

paper: https://arxiv.org/pdf/2411.02337
github: https://github.com/THUDM/WebRL
ICLR 2025 accepted (인용수: 9회, ‘25-06-24 기준)
downstream task: webarena

1. Motivation

기존의 LLM기반 Web agents는 대부분 조작된 prompt와 LLM API를 활용하여 web page를 이해하고 조작했는데, 이는 비용이 비싸고, 시간이 오래걸린다.
Sparsity & cost of feedback signals: open-source LLM은 pretraining/post-training 시에 decision-centric data의 부족으로 전문적인 web agent 수준에 성능이 미치지 못한다.
Insufficienty of training tasks: 최근에 Imitation learning (SFT) 기반으로 연구가 시도 되었으나, web interaction의 online nature를 반영하기에는 데이터의 양이 불충분하고, continual improvement가 힘들다.
Policy Distribution drift in online learning: 학습 중에 catastrophic forgetting이 생길 수 있다.

$\to$ 이러한 문제를 해결하기 위해 WebRL framework를 제안해보자!

2. Contribution

새로운 자가 발전하는 LLM기반 web agent로서, Curriculum RL framework인 WebRL을 제안함
- WebArena 환경에서 최초로 RL을 도입했음
- ORM (Output-supervised Reward Model) 적용
3가지 핵심 challenge를 풀고자 했음
- 학습 task의 부족 $\to$ Self-evolving curriculum & adaptive learning 전략
- Feedback signal의 sparsity $\to$ confidence 기반의 threshold 조절
- Distribution shift $\to$ KL Divergence + Experience replay buffer
WebArena-benchmark에서 SOTA를 달성함
- Chatgpt보다 160% 성능이 우수함

3. WebRL

Framework
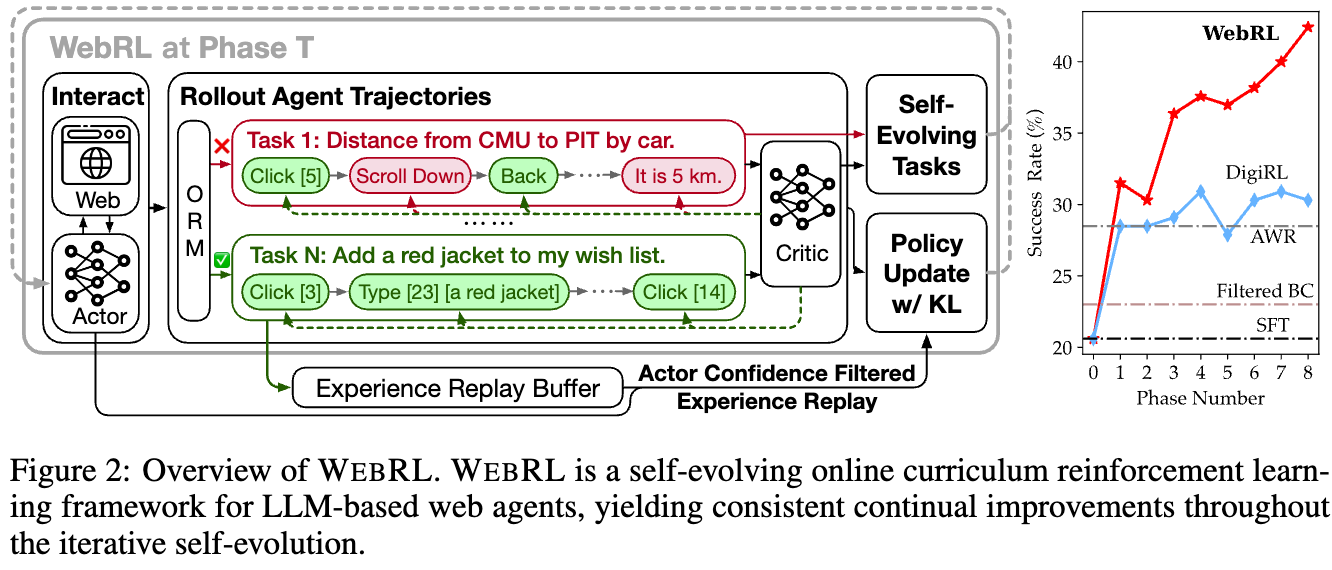
- Agent는 지속적으로 Environment와 상호작용하면서 실시간 trajectory data를 취합함.
- 해당 상호작용은 Agent의 현재 상태에서의 proficiency를 고려하여 Self-evolving curriculum 전략에 가이드를 받아 진행됨
- ORM (Outcome-supervised Reward Model) 역시 학습하여 task의 success를 평가함
- KL-Constraint + Relpay buffer를 두어 polciy update algorithm을 조절하여 극단적인 policy shift를 방지함
Algorithm
- 학습 pipeline: SFT $\to$ 1st RL $\to$ 2nd RL $\to$ … $\to$ Nth RL
  - 매 step마다 이전 step의 policy 모델로 replay buffer / failure set을 모아둠
    - 500개의 task를 GPT-4o로 filtering하여 생성 (perplexity 1/0.95 ~ 1/0.5사이)
    - actor / critic을 학습
ORM(Outcome-supervised Reward Model) Training
- 역할: 에이전트의 행동 궤적(trajectory)이 주어진 작업을 성공적으로 완료했는지 여부를 평가하는 모델
- 목적: WebArena와 같은 온라인 환경에서는 에이전트가 작업을 성공했는지 즉각적인 피드백을 받기 어렵기 때문에, ORM을 사용하여 작업 성공 여부를 판단하고 에이전트에게 보상 신호(성공 시 1, 실패 시 0)를 제공
- 활용: WEBRL 프레임워크의 커리큘럼 학습 과정에서 새로운 작업이 생성될 때, 이 작업에 대한 에이전트의 수행 결과를 평가하고 보상을 제공하는 데 필수적으로 사용됩니다. 이는 훈련 작업의 부족 문제와 희소한 피드백 신호 문제를 해결하는 데 기여
- 훈련: HTML 내용, 에이전트의 행동 기록, 사용자 지침 등을 입력으로 받아 작업 완료 여부를 “YES” 또는 “NO”로 출력하도록 훈련
  - WebArena에서 제공하는 1,186 training sample과 더불어, rollout을 추가로 수행하여 12,200 sample을 가지고 학습을 수행
- WebRL은 학습된 ORM 모델을 활용하여 Reward signal을 도출함

3.1 Self-Evolving New Instruction for Curriculum Learning

매 Phase마다 (Curriculum Learning으로) task를 생성하면서 학습 task부족 이슈를 해결함
학습이 진행될수록, task의 난이도는 상승함
2 step approach를 사용
- generation step: in-breadth evolving approach를 사용하여 이전 interaction phase들에서 fail한 task를 seed로 활용하여 새로운 instruction을 생성함
- filtering step: 학습된 critic 모델을 활용하여 생성된 instruction중, 해당 환경과 align되어 있고, 요구되는 어려움 난이도가 feasible한 것만 남기게 함
  - critic score가 0.05 ~0.75 사이에 존재해야 함.
  - 수동으로 생성된 task를 분별하여 WebArena에서 수행하지 못하는 task를 걸러넴
    
    $\to$ GPT를 써서 해당 infeasible task를 제외시킴

3.2 Reinforcement Learning for LLMs in Online Web Environments

정책 모델 목표함수

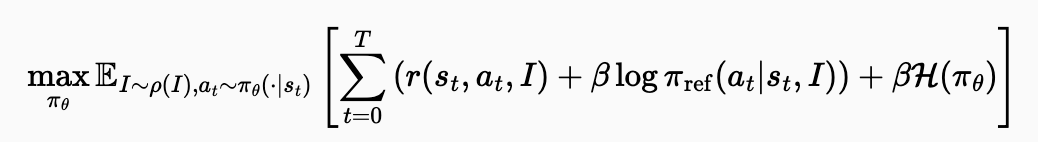
$max_{\pi_\theta}$: 정책 $\pi_\theta$의 매개변수 $\theta$에 대해 수식의 값을 최대화합니다.

$\mathbb{E}{I \sim \rho(I),a_t \sim \pi\theta(\cdot

s_t)}$: 목표 함수의 값은 현재 단계의 작업 분포 $\rho(I)$에서 추출된 instruction I와, 현재 정책 $\pi_\theta$에 따라 상태 $s_t$에서 추출된 행동 $a_t$에 대한 기대값. 즉, 다양한 작업 환경에서 현재 정책을 따랐을 때의 평균적인 결과를 의미.

$\sum_{t=0}^T$: 시간 단계 (t=0)부터 종료 시간 (T)까지의 합산. 각 시간 단계에서 얻는 보상과 정책 관련 항을 누적.
$r(s_t, a_t, I)$: 시간 t에 상태 $s_t$에서 행동 $a_t$를 취하고 instruction I를 따랐을 때 얻는 보상. 웹 에이전트 태스크에서는 일반적으로 작업 성공 시에만 마지막 단계에서 1의 보상을 받고, 그 외에는 0의 보상을 받는 희소(sparse)한 형태임.

$\beta \log \pi_{\text{ref}}(a_t

s_t, I)+\beta\mathcal{H}(\pi_\theta)$: 이 항은 현재 정책 $\pi_\theta$가 이전 단계의 정책 $\pi_{\text{ref}}$에서 크게 벗어나지 않도록 제약하는 역할 수행. $\beta$는 이 제약의 강도를 조절하는 계수. 이 값을 최대화하는 것은 $\pi_\theta$와 $\pi_{\text{ref}}$ 간의 KL-divergence를 최소화하는 것과 관련이 있음. 이는 온라인 학습 중 발생하는 정책 분포 드리프트(policy distribution drift)를 완화하여 안정적인 학습에 기여함.

$\to$ 이렇게 학습된 모델을 최적 정책 모델이라고 함 ($\pi^*$)

정책 모델($\pi_{\theta}$) 손실 함수

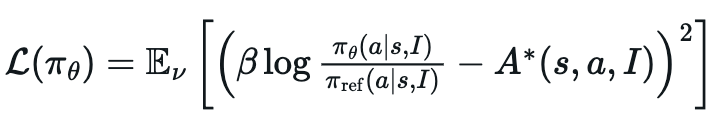
$\mathcal{L}(\pi_\theta)$: 학습 목표인 정책 손실 함수. 이 값을 최소화하는 방향으로 현재 정책 $\pi_\theta$의 매개변수 $\theta$를 업데이트 수행.
$\mathbb{E}_{\nu}[\dots]$: 경험 분포 $\nu$에 대한 기댓값. 여기서 경험 분포 $\nu$는 현재 학습 단계에서 수집된 상호작용 데이터와 replay buffer에서 가져온 과거 경험 데이터의 분포를 의미
$(\beta)$: KL-divergence 제약의 강도를 조절하는 계수. $\beta\beta$ 값이 클수록 현재 정책 $\pi_\theta$가 참조 정책 $\pi_{\text{ref}}$에서 크게 벗어나지 않도록 강하게 제약

$\log \frac{\pi_\theta(a

s, I)}{\pi_{\text{ref}}(a

s, I)}$: 현재 정책 $\pi_\theta$와 참조 정책 $\pi_{\text{ref}}$ 하에서 특정 상태 (s)와 지침 (I)가 주어졌을 때 행동 (a)를 선택할 확률의 로그 비율. 이 항은 두 정책 간의 KL-divergence와 관련되어 정책 분포 드리프트를 제어하는 역할을 수행

$A^*(s, a, I)$: 상태 (s)와 지침 (I)에서 행동 (a)를 수행했을 때의 optimal advantage 함수. Advantage 함수는 특정 상태에서 어떤 행동을 취했을 때의 가치가 해당 상태의 평균 가치보다 얼마나 더 나은지를 나타냄. WEBRL에서는 이 advantage 함수를 value 네트워크 V를 사용하여 추정.

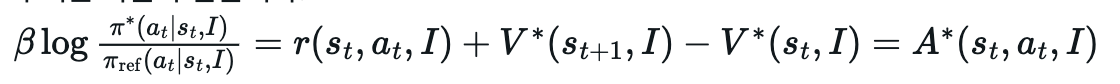
$\log \frac{\pi^*(a_t

s_t, I)}{\pi_{ref}(a_t

s_t, I)}$: 현재 상태 $s_t$에서 주어진 지침 I에 따라 행동 $a_t$를 취할 때, 최적 정책 $\pi^*$와 이전 정책 $\pi_{ref}$ 간의 확률 비율에 로그를 취한 값. 이는 두 정책 간의 KL-divergence와 관련이 있으며, 두 정책이 얼마나 다른지를 나타내는 지표로 사용될 수 있음.

$\pi^*(a_t

s_t, I)$: 상태 $s_t$에서 지침 I에 따라 행동 $a_t$를 취할 최적 정책의 확률.

$\pi_{ref}(a_t|s_t, I)$: 상태 $s_t$에서 지침 I에 따라 행동 $a_t$를 취할 이전 정책의 확률. 이 논문에서는 이전 학습 단계의 정책을 의미.
$r(s_t, a_t, I)$: 상태 $s_t$에서 지침 I에 따라 행동 $a_t$를 취했을 때 받는 즉각적인 보상(reward). 이 논문의 WebArena 환경에서는 중간 단계 보상은 0이고, 최종 작업 성공 시에만 1을 받음.
$V^*(s_{t+1}, I)$: 다음 상태 $s_{t+1}$에서 지침 I에 따라 얻을 수 있는 기대 누적 보상의 최적 가치 함수(Optimal Value Function) 값.
$(V^*(s_t, I)$: 현재 상태 $s_t$에서 지침 I에 따라 얻을 수 있는 기대 누적 보상의 최적 가치 함수 값.
$r(s_t, a_t, I) + V^(s_{t+1}, I) - V^(s_t, I)$: 상태 $s_t$에서 행동 $a_t$를 취했을 때 얻는 즉각적인 보상에 다음 상태의 가치를 더한 값과 현재 상태의 가치 간의 차이. 이는 시간 차이(Temporal Difference, TD) 오차의 형태를 가지며, 해당 행동이 현재 상태 가치 추정치보다 얼마나 더 나은지를 나타냄.
$A^*(s_t, a_t, I)$: 상태 $s_t$에서 지침 I에 따라 행동 $a_t$를 취하는 것의 최적 어드밴티지 함수(Optimal Advantage Function) 값. 이는 해당 상태에서 취할 수 있는 평균적인 행동보다 특정 행동 $a_t$가 얼마나 더(또는 덜) 좋은지를 나타냄.

가치 모델 (V) 손실 함수
- 목적: 주어진 action, instruction, state를 보고 reward를 예측하는 모델
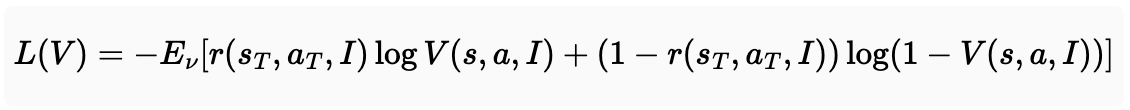
- $L(V)$: 가치 네트워크 V의 손실 함수.
- $E_{\nu}[\dots]$: 데이터 분포 ($\nu$)에 대한 기대값. 데이터 $\nu$는 학습 과정에서 수집된 궤적들로 구성.
- $r(s_T, a_T, I)$: 마지막 상태 $s_T$에서 행동 $a_T$를 통해 얻은 보상. 여기서는 작업 성공 시 1, 실패 시 0의 이진 보상.
- $V(s, a, I)$: 가치 네트워크가 예측하는 특정 상태 s, 행동 a, 명령어 I에 대한 가치. 이 손실 함수에서는 주로 최종 상태에서의 성공 확률을 예측하는 데 사용.
- $\log V(s, a, I)$: 가치 네트워크가 성공(보상 1)을 예측할 확률의 로그값.
- $\log(1 - V(s, a, I))$: 가치 네트워크가 실패(보상 0)를 예측할 확률의 로그값입니다.
Replay Buffer
- 이전 iteration에서 학습된 모델을 actor로 하여 successful trajectories에 한해 buffer에 저장함
- 단, 불확실성이 1/0.95 ~ 1/0.5 사이인 task (== 너무 어렵지도, 너무 쉽지도 않은 task)만 남기고, 나머지는 학습에 필터링하여 미활용

4. Experiments

Evaluation benchmark
- 165 test tasks of WebArena-Lite
Baselines
- GPT-4-Turbo / GPT-4o
- Llama-3.1 / GLM-4-9B
State space
Action Space
정량적 결과
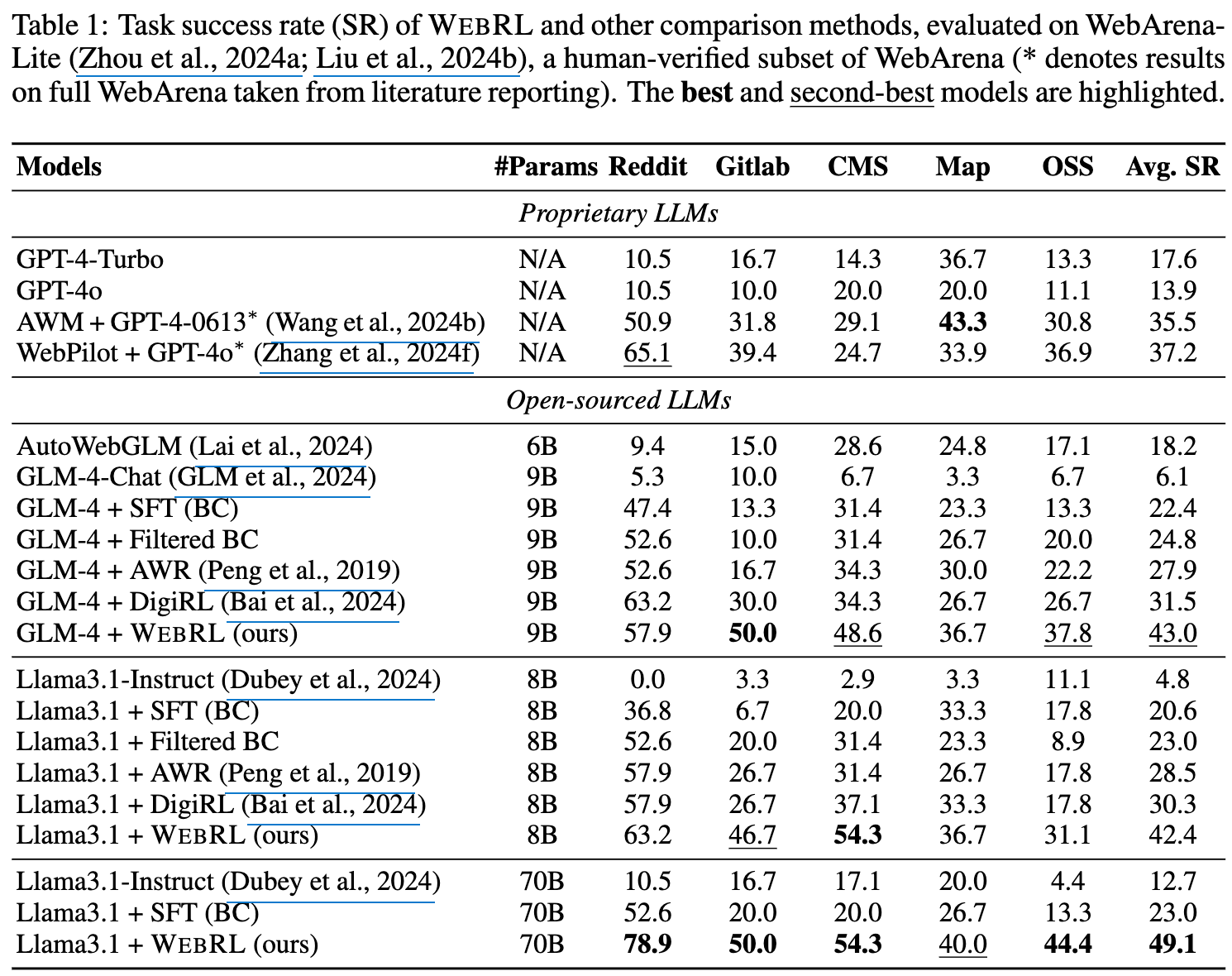
- Scaling Effect of WebRL
  - Llama-3.1-7B $\to$ Llama-3.1-70B로 바꾸면 성능이 향상됨 (42.4% $\to$ 49.1%)
Error 유형 분석
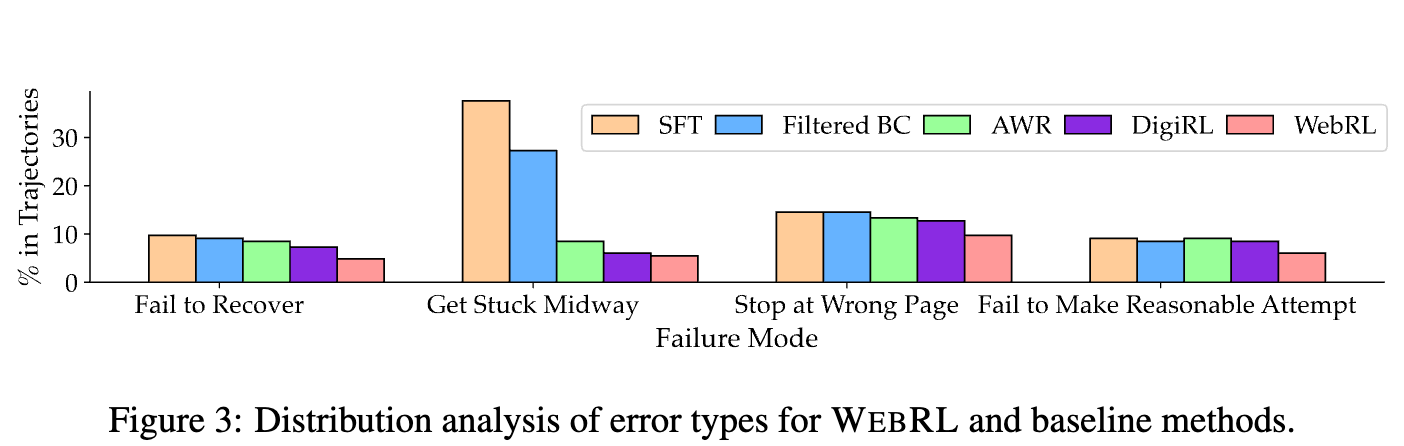
요구되는 step에 따른 Task Performance 분석
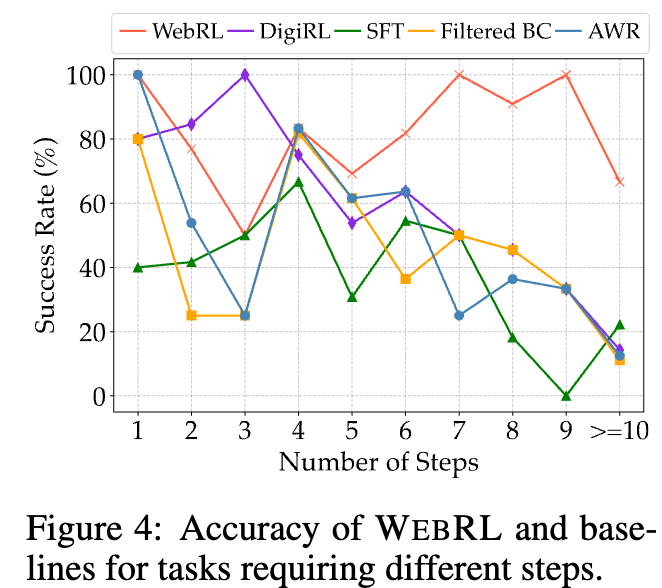
- 요구되는 step 정의:= 각 모델들 중에 가장 적은 step으로 성공한 step
  - 즉, 모든 모델이 실패한 task는 제외
- DigiRL: medium-task에서 좋은 성능을 내지만 long-task(>10회 이상) 잘 안됨 $\to$ fixed set of task 때문으로 추정
- WebRL: long-task에서도 좋은 성능 $\to$ curriculum learning으로 long task도 잘풀게됨
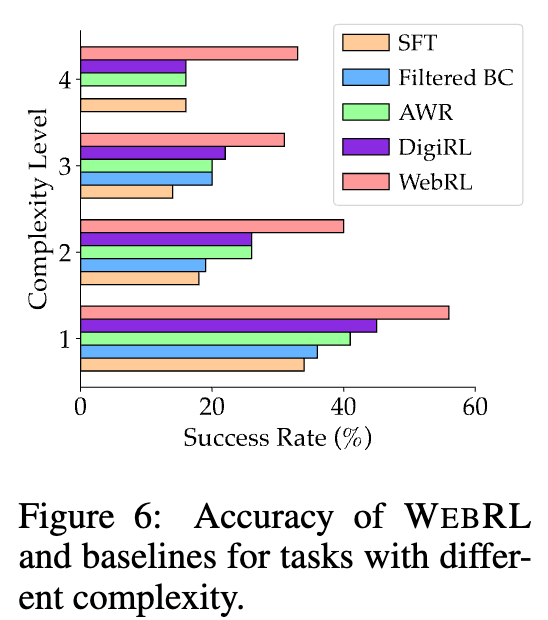
다양한 Task Complexity에 따른 성능 분석
- Task Complexity := Instruction에서 찾아야 하는 요구사항의 갯수
  
  ex. “What are the top-3 best-selling products in Jan 2023” $\to$ 2개
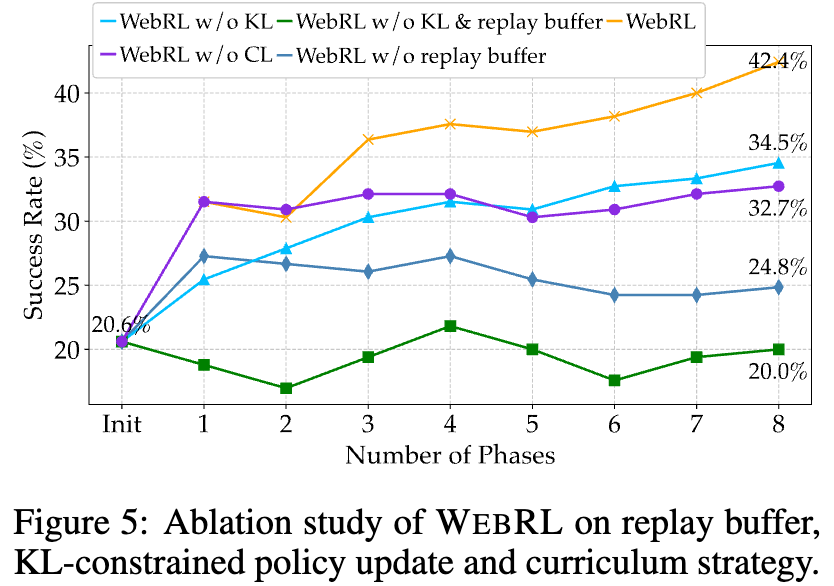
Ablation Studies
- Replay buffer / KL-constrained update / curriculum learning전략 유무에 따른 성능 분석
- Perplexity에 따른 성능분석
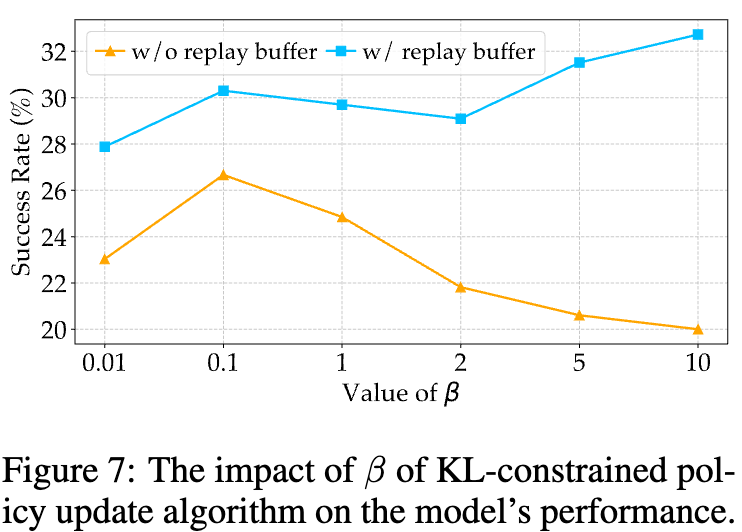
- $\beta\beta$ & Replay Buffer 유무에 따른 성능 분석
ORM (Reward Model) 평가
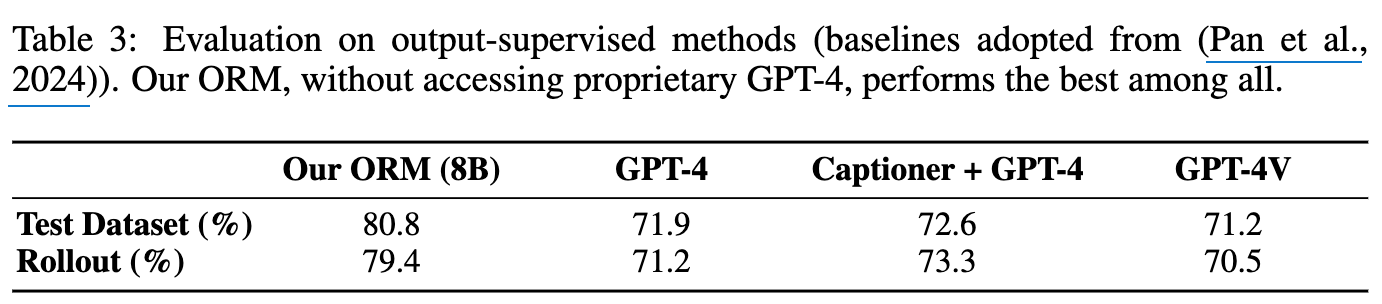
- Policy 모델의 interaction trajectory를 토대로 reward를 계산하는 매우 중요한 모델임
- GPT-4-Turbo. + Captioner vs. GPT-4V를 WebArena-Lite teset set 중 100개의 sampled rollout을 수동으로 label한 걸로 평가
Case Study
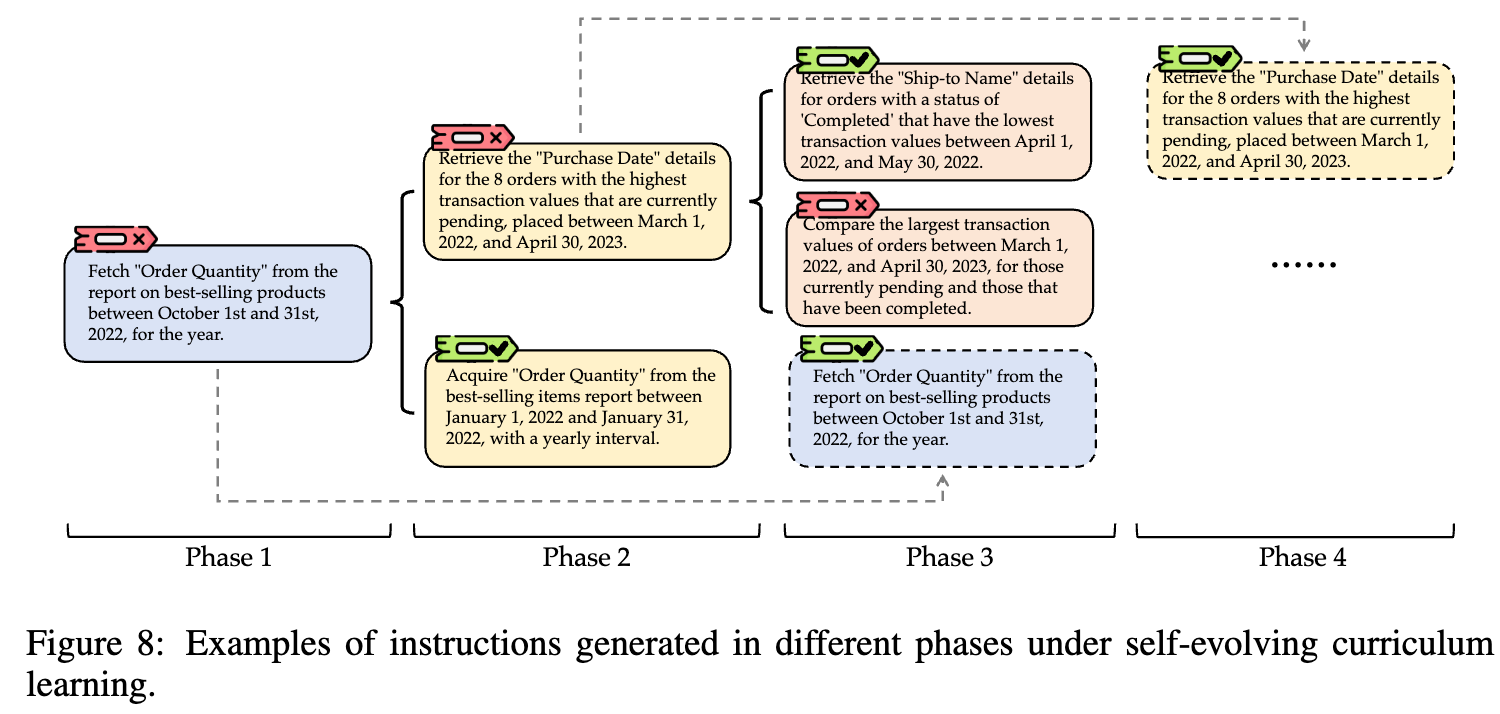
- Phase 1에서 틀린 task $\to$ Phase 2에서는 모호한 것을 분명히 하여 task를 해결하도록 수행 (“yearly interval”)
  - Phase 2를 학습한 모델은 동일한 task (Phase 1)를 다음 step (Phase 3)에서는 성공적으로 학습하게 됨
- 이전에 맞춘 task는 다음 step에서는 더욱 어렵게 만들어 해결하게 되어, 성능이 오름