[TTA][CLS] TEA: Test-time Energy Adaptation

2 minute read

[TTA][DG][CLS] TEA: Test-time Energy Adaptation

paper: https://arxiv.org/abs/2311.14402
github: x
archived (인용수: 0회, ‘24-01-26 기준)
downstream task: TTA for CLS, DG for CLS

1. Motivation

covariance shift를 해결할 묘책이 현재로선 없었음
probability score의 sum of negative log likelyhood 를 energy로 정의하고, energy를 최소화하는 방향으로 Landenvien Gradient Dynamics를 활용하여 target에 adapt된 특성을 모델이 학습함으로써 한계점을 풀어볼 수 있지 않을까?
- lower energy $\to$ higher probability score
- (UDA)처럼 source 접근이 필요없고, (TTT)처럼 training process에 변화가 필요없는 simple한 방식임
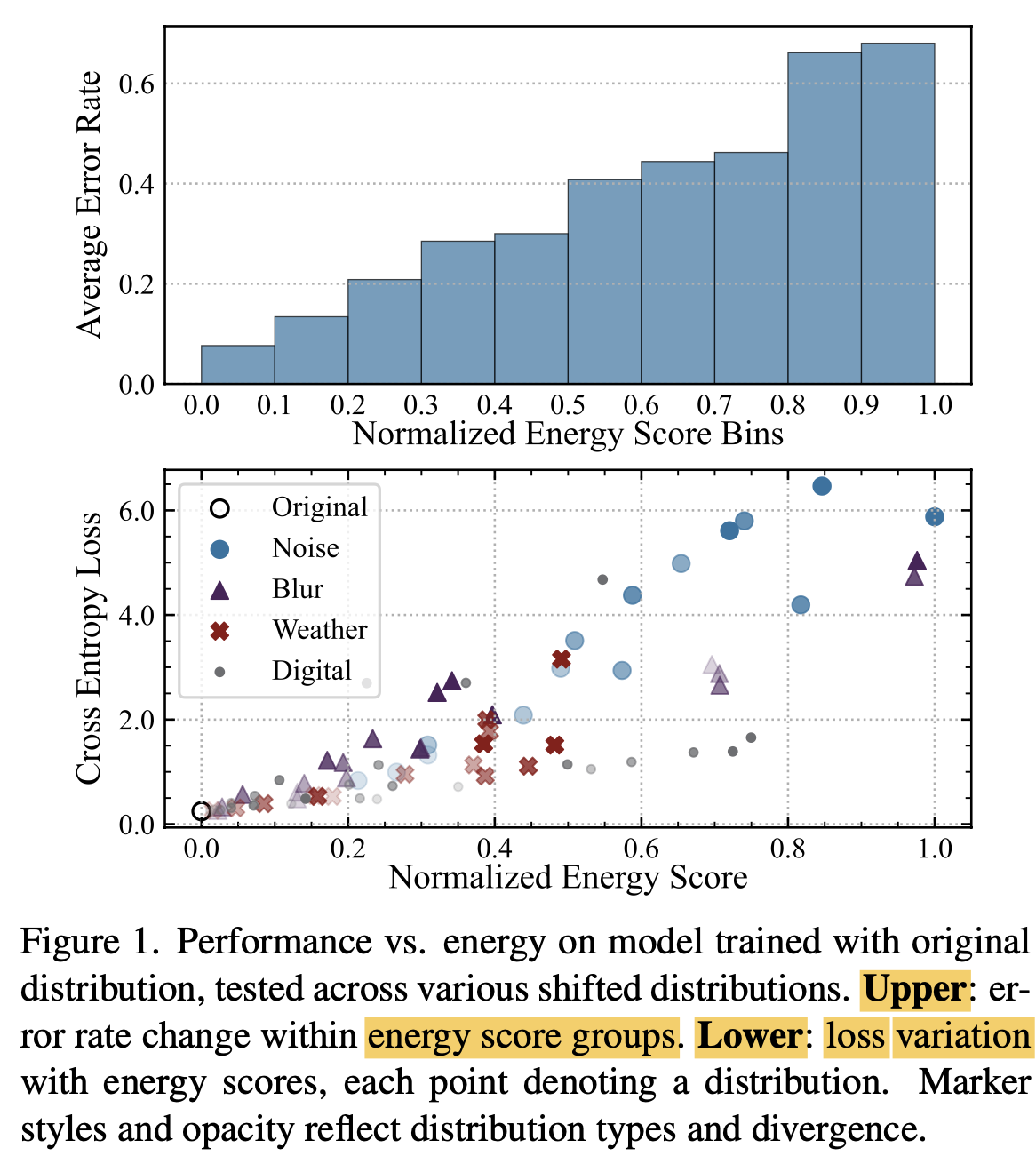
- (Upper) ECE (Expected Calibration Error)가 낮다
- (Lower) Covariance Shift가 높은 (투명도가 낮은) dataset들이 normalized energy score가 높고, CE Loss가 낮음

2. Contribution

TTA에 Energy-based 방식을 새롭게 제안하여 domain shift를 해결
- Test data에 대한 energy를 최소화하는 방향으로 model의 distribution을 (normalization layer parameter)를 업데이트함으로써 test distribution에 대해 generalization 성능을 향상시킴
- MinMax Game
  - discriminator : test sample에 대한 probability를 maximize하기 위해 Contrastive Divergence 도입
    - test sample의 energy와 모델 본연의 distribution간의 energy를 L2 loss로 설계
  - generated sample (모델 본연의 distribution)은 energy를 minimize하도록 Stochatic Gradient Langevin Dynamics (SGLD)로 학습
TTA, DG for CLS benchmark에서 SOTA

3. TEA

Overall Architecture
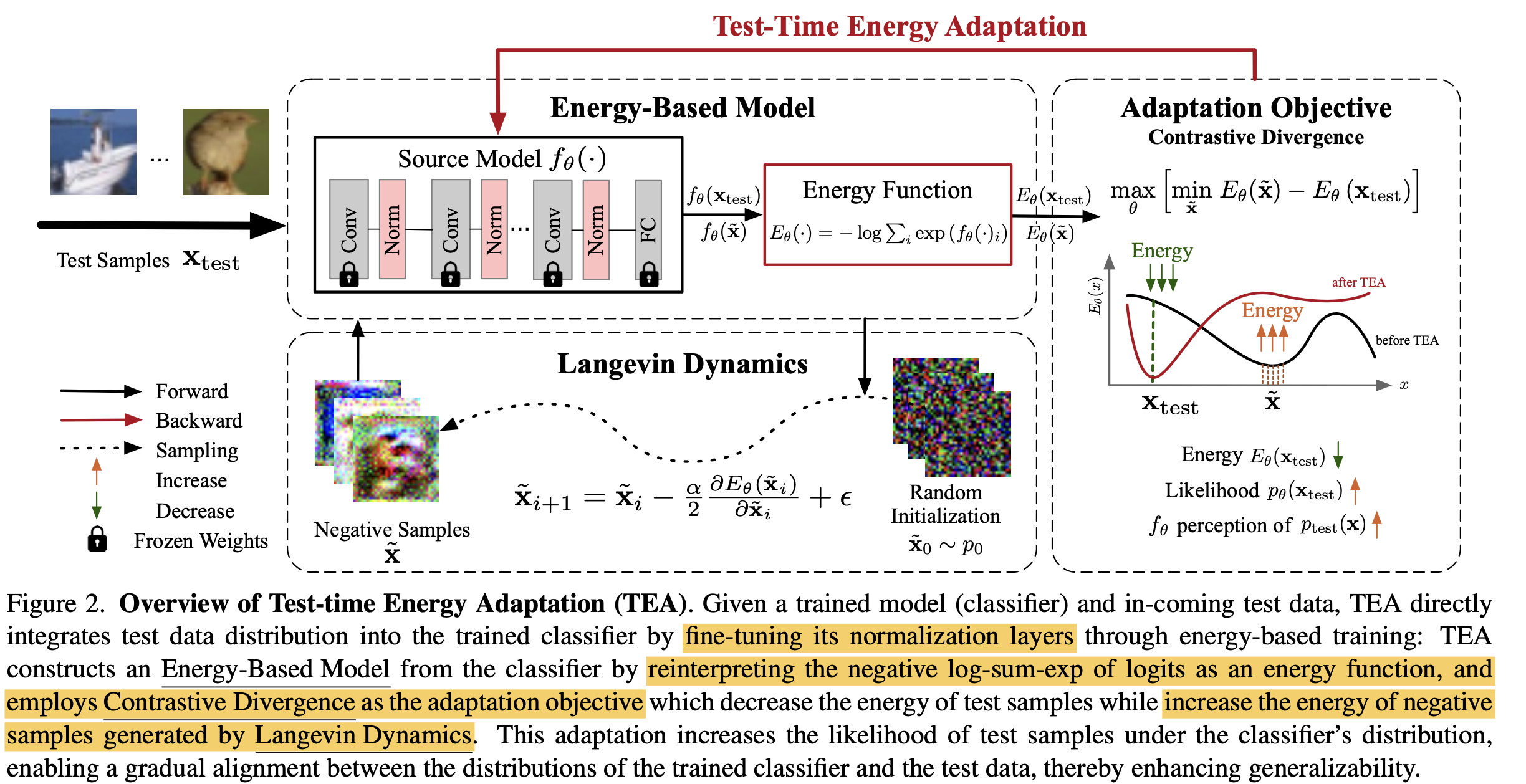
- Energy: Energy-based Model이 입력 x에 대해 scalar 값으로 mapping해주는 함수
  \[E: \mathbb{R}^D \to \mathbb{R}\]
  - Boltzman distribution
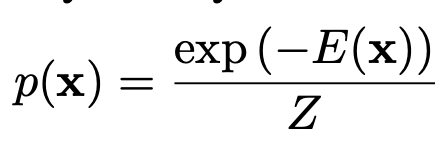
  - Energy-based Model의 기저에는 sample x에 대한 임의의 classificaiton logit y로 표현할 수 있다고 가정
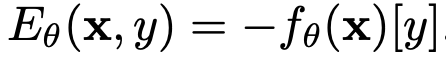
  - x, y의 joint probability 분포는 Boltzman distribution에 의해 표현될 수 있음
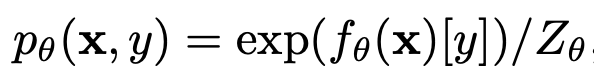
  - x의 distribution은 y에 대해 marginalize해서 (y를 제거함으로써) 구할 수 있음
    
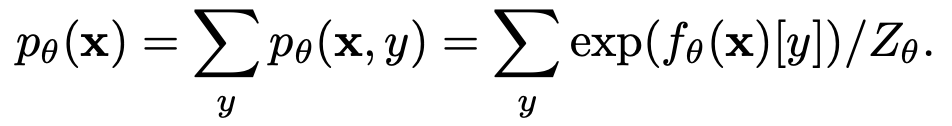
    $\to$ Boltzman식에 대입하여 E에 대해 정리하면
- Energy: Negative loglikelyhood of model’s logit y.
  - 위 식을 Boltzman distribution에 대입하여 Energy에 대해 정리
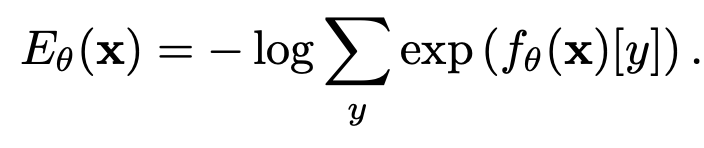
- test sampel x에 대한 Energy는 최종적으로 아래와 같다.
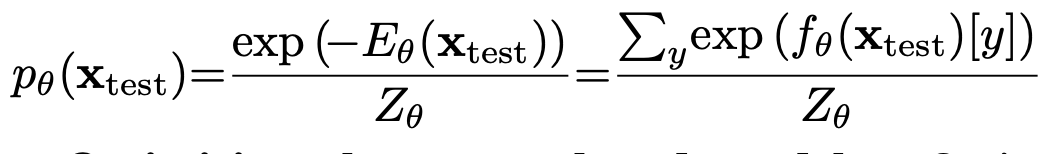
  - $\sum_yf_{\theta}[y]$: energy-based model의 classification y에 대해 marginalize한 값
- How to Optimize Energy?
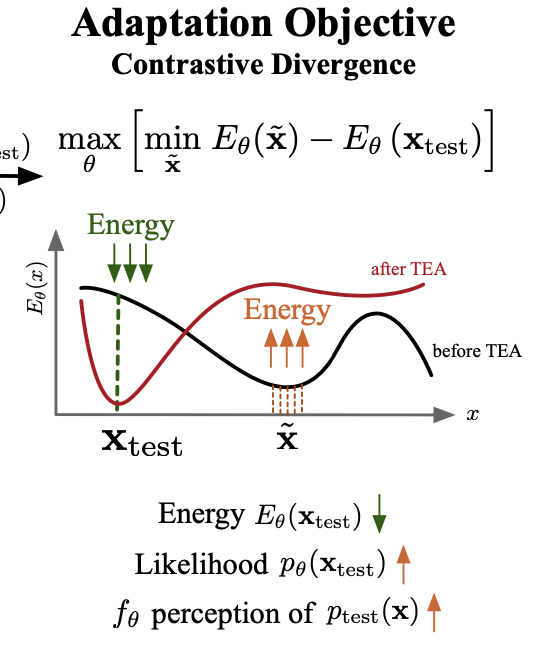
  - Source data로 trained된 모델과 test data간의 distribution을 align시키기 위해 test data를 pretrained model을 통과해 얻은 energy와 random noise를 pretrained model을 통과시켜 얻은 energy에 대해 contrastive divergence를 최소화 하도록 loss를 설계함
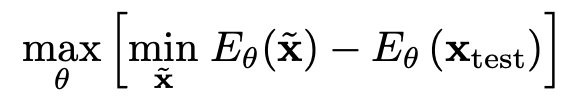
    - $\tilde{x}$: random noise에서 denoising을 거쳐 생성된 discriminator의 generated sample
    - $x_{test}$: test sample
      
      ($\to$ test sample에 대한 (source-only trained)모델의 energy는 높고, generated된 sample에 대한 energy는 SLGD minimize에 의해 minimize되었기에 낮으므로, 두 값의 차이를 극대화하는게 곧, 두 energy 차이를 최소화하는 방향이라 생각이 듦)
  - energy optimization $\to$ intractable한 unnormalized probability를 directly optimize하는 대신, 그 gradient를 최소화
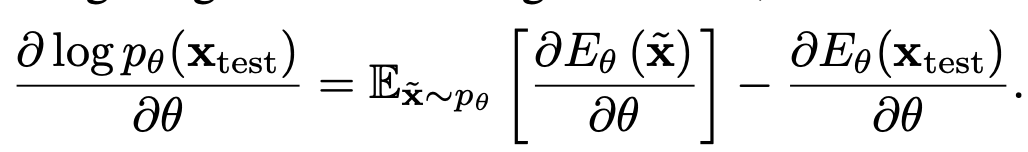
    - model parameter $\theta$ 에 대해 미분
  - 위 probability 를 directly maximize하는 것은 어려우므로, Log gradient를 maximizeg
    - Sampling process : Stochastic Langenvien Gradient Dynamics (SLGD)
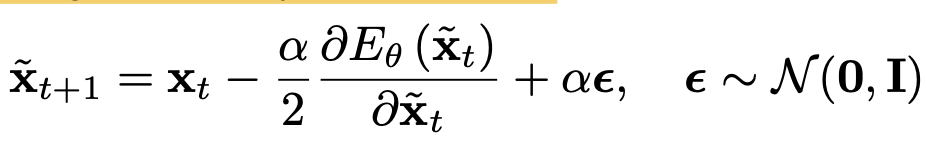
      - generated sample $\tilde{x}_t$에 대해 미분
      - $\alpha$: step-size
      - t: time step
      - x_t: t step의 generated image. initial value = random noise
        
        $\to$ target domain에 무관하게 energy를 minizmie하는 term. $\to$ trivial solution으로 mode collapse하는 것 방지
Overall Algorithm

4. Experiments

TTA benchmarks with WRN-28-10
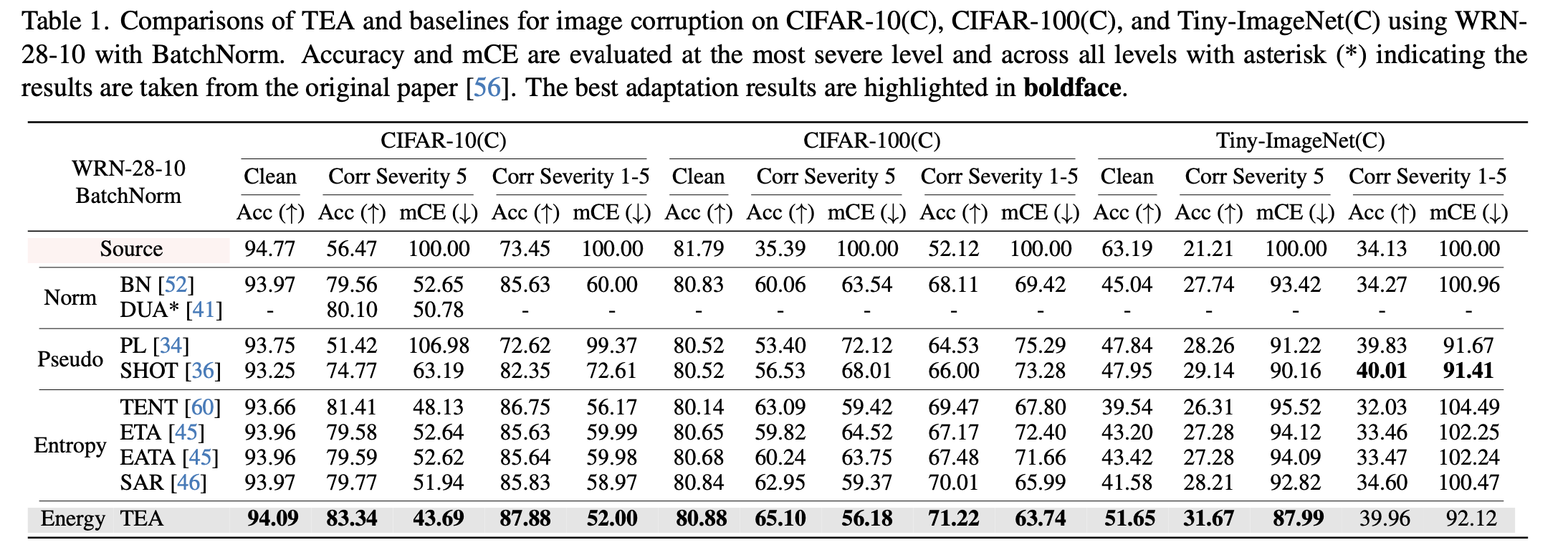
TTA benchmarks with Res50
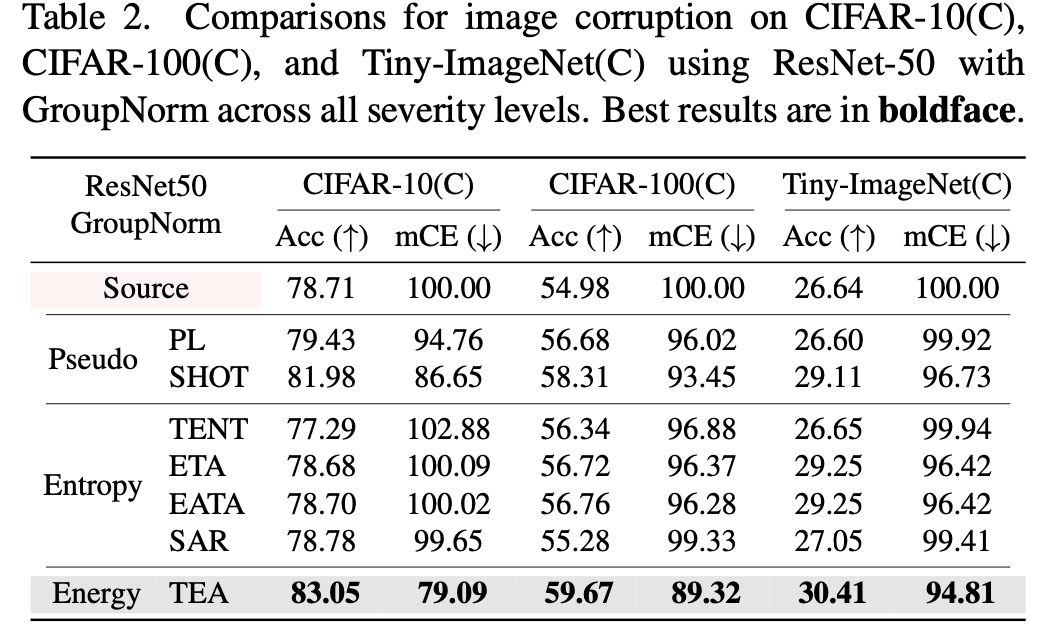
Single Source DG benchmark
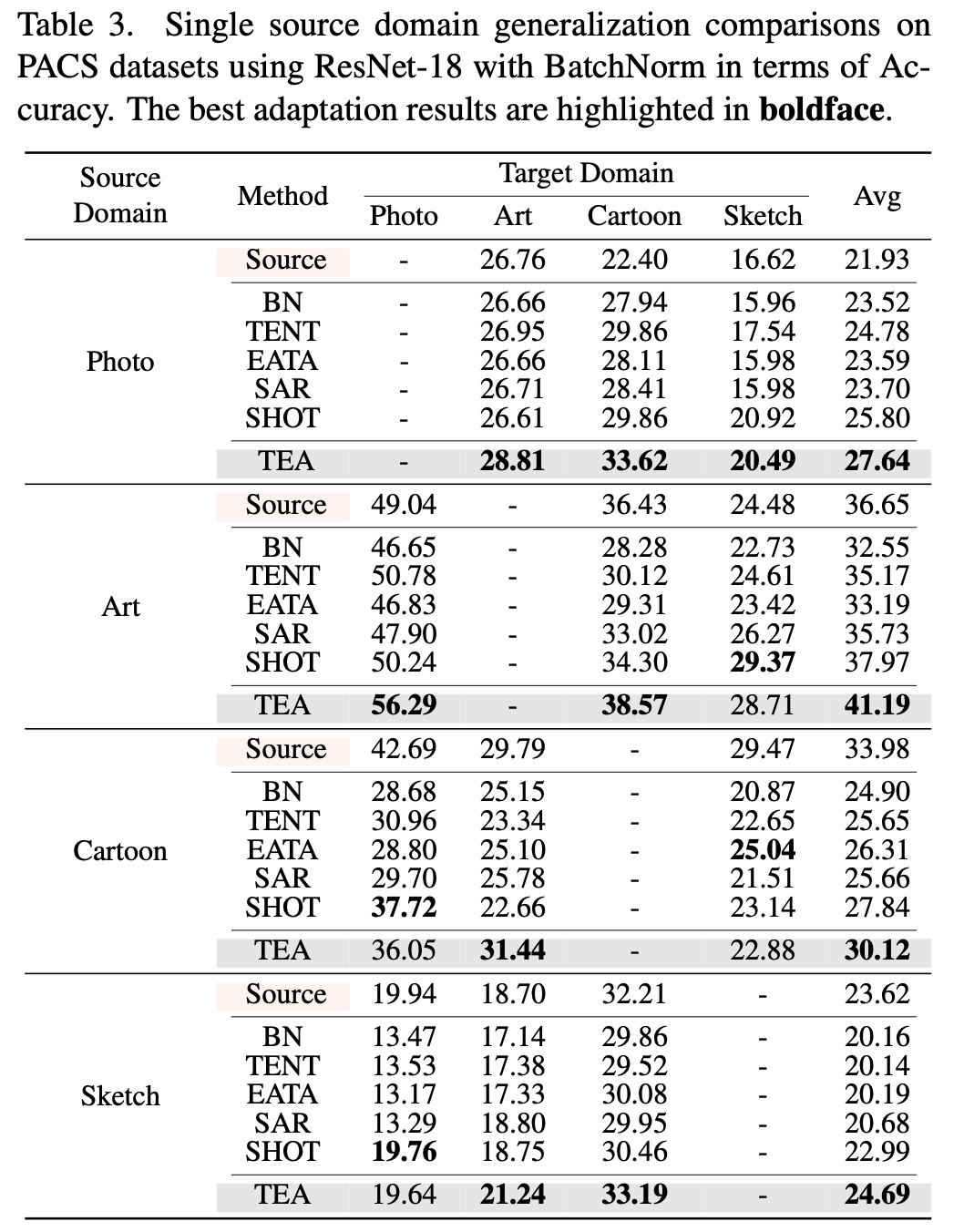
Enery reduction과 accuracy, CE Loss 관계 분석
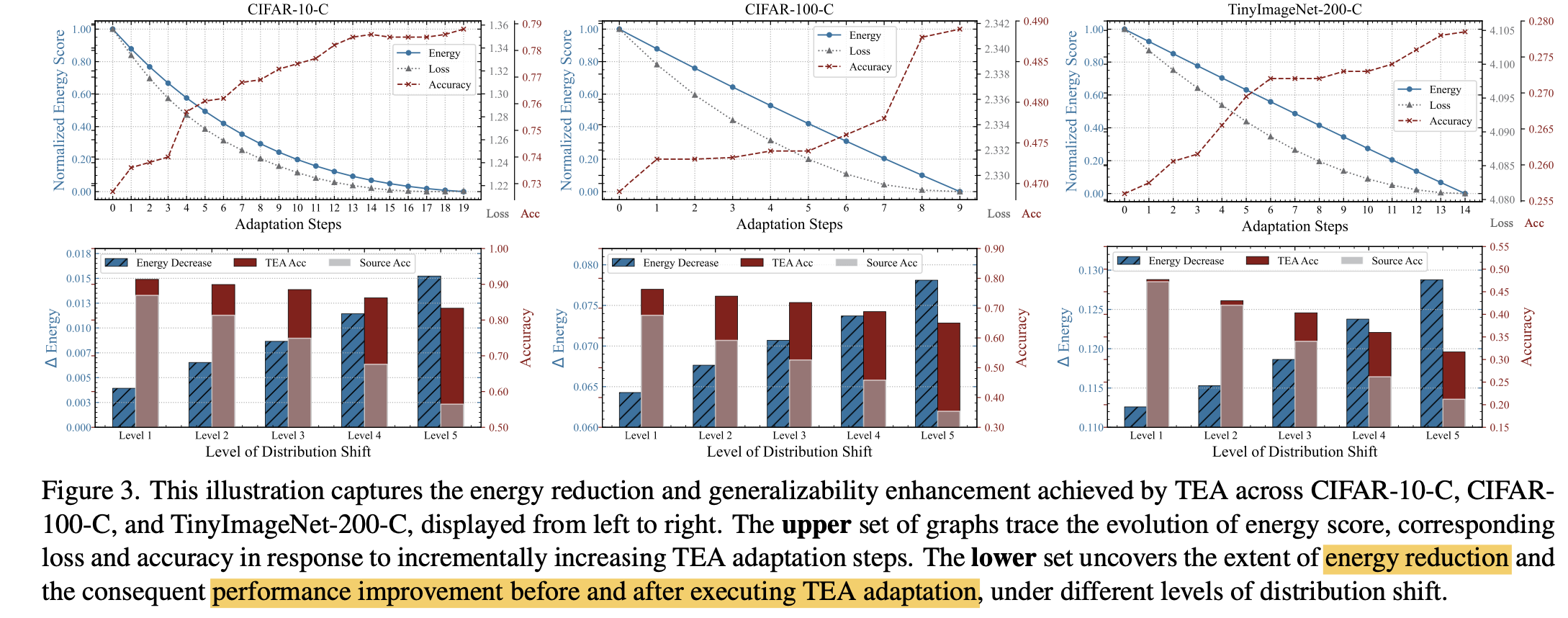
- (1행) step이 진행됨에 따라 energy가 감소하고, accuracy는 증가, Loss도 감소함
- (2행) distribution shift level (higher $\to$ more distribution shift)한 protocold에서 energy reduction이랑 accuracy 증가폭이 크다
TEA의 TTA benchmark에서 generation된 이미지 분석

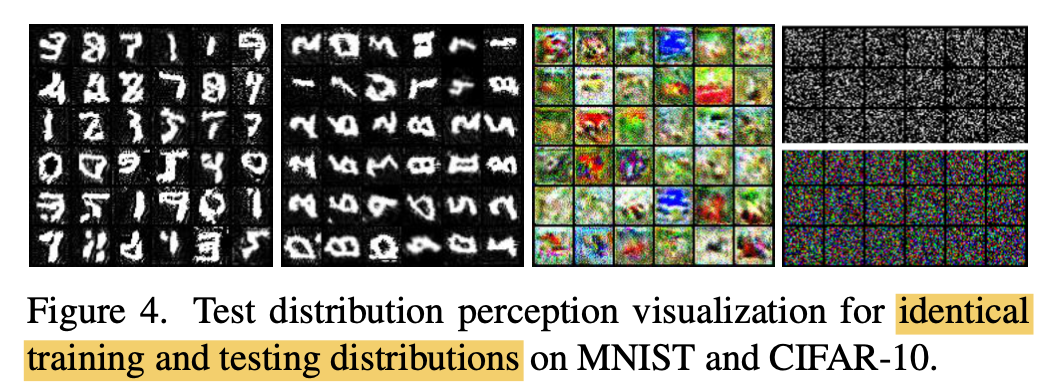
(1, 3) train/test domain이 identical한 경우 (MNIST, CIFAR-10)을 제대로 recontruct하고 있음 $\to$ domain 특성을 잘 학습했다

(2) train/test domian이 cov. shift가 있는 경우 (MNIST vs. 90도 튼 MNIST)에도 TEA는 제대로 recontruct하고 있음 $\to$ domain pattern 특성을 잘 학습했다

(4) train/test domian이 cov. shift가 있는 경우 (MNIST vs. 90도 튼 MNIST)에도 TEA adaptation을 수행하지 않은 경우는 제대로 recontruct하고 있지 못함
TEA의 DG benchmark에서 generation 이미지 분석
- domain shift가 있는 single source DG benchmark에서도 잘된다.
TEA의 ECE 분석
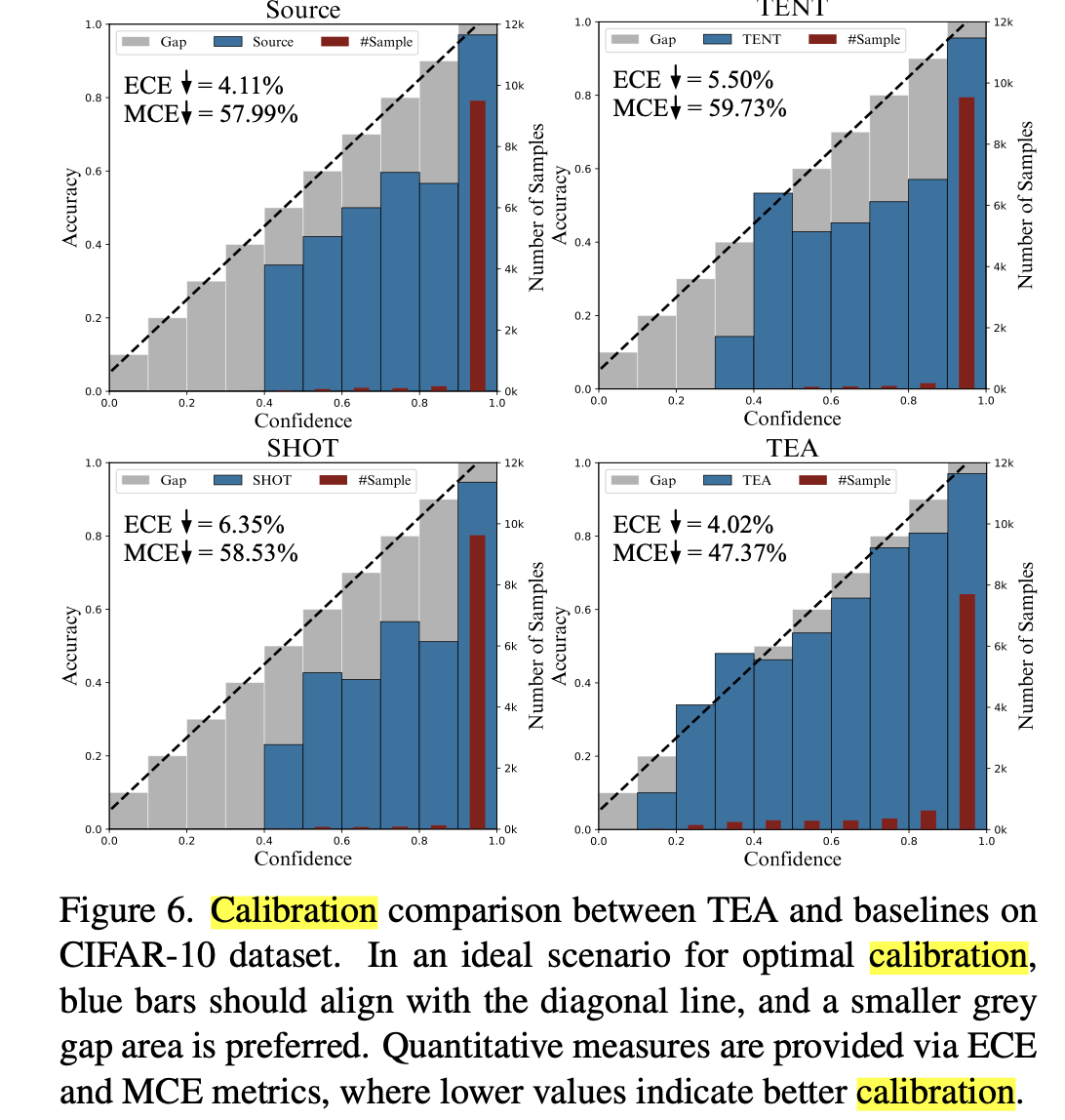
- 기존 방식들 (TENT, SHOT)은 GT class에 대한 entropy만 최소화하도록 학습하고, 다른 class에 대해서는 entropy가 없다는 (극단적?) 가정을 함
- TEA의 negative log likelyhood maximization은 각 class에 대한 uncertainty를 부여하게 되므로, calibration error를 줄이게 된다. (현실적이다?)