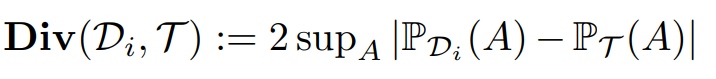[DG][CLS] SWAD: Domain Generalization by Seeking Flat Minima

[DG][CLS] SWAD: Domain Generalization by Seeking Flat Minima

• paper : https://arxiv.org/abs/2102.08604
• github : https://github.com/khanrc/swad
• NeurIPS 2021 (인용수 148회 , ‘23.07.09 기준)
• task : Domain Generalization for Classification

Abstract

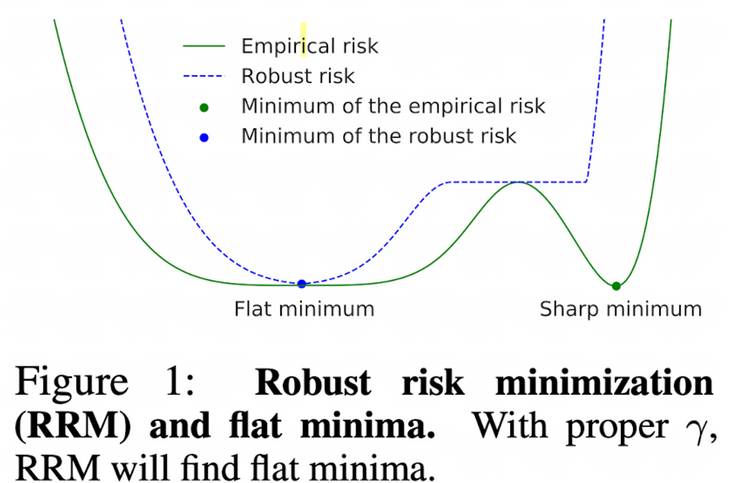
• 문제제기: 기존의 ERM (Empirical Risk Minimization)으로 non-convex loss funtion의 sharp minima로 수렴시키는 학습기법은 generalizability를 해친다.
• 제안점 : loss function의 flat minima를 찾는 것이 domain generalization gap을 줄이는 것임을 이론적으로 보임
• SWAD (Stochastic Weight Averaging Densely)를 제안하여 기존의 SWA 보다 flatten minima에 수렴함을 보임. (+ less overfitting)
  • 차별점 : dense하게 average를 하되, overfit-aware하게 stochastic weight sampling 전략을 취함
• DG for classification Dataset 5개에서 SOTA를 찍음

1. Introduction

• 기존 연구의 한계점
  • ERM으로 학습함 → Sharp minima에 빠지면 i.i.d. 상황이 아닌 DG상황에서는 domain shift로 인해 loss curve가 달라지므로 generalizability가 훼손됨
  • flat minima가 generalizability를 향상시킨다는 연구들도 모두 i.i.d.상황을 가정함 → DG상황은 generalizable gap이 flat minima와 sharp minima가 크게됨
• 제안점
  • flat minima가 unseen domain에서 더 generalizable함을 보이기 위해 RRM (Robust Risk Minimization)을 정의함
    • RRM: neighbor parameter space 상에서 worst-case empirical risk임
      • generalization gap of DG의 Upper bound
  • SWAD : 기존에 flat minima를 잘 해결하는 SWA (Stochastic Weight Averaging)에서 두 가지를 변형함
    • densly : epoch based에서 iter based로 weight averaging
    • overfit-aware averaging : validation loss를 기준으로 overfit을 방지하도록 averaging

2. Theoretical Relationship b/w Flatness and DG

• Loss의 최적 해는 여러가지 있을 수 있음

• 근데 기존 방법 (ERM)은 sharp minima로 수렴할 수 있음

  

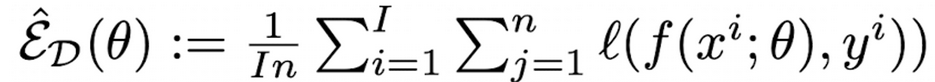
  • n : source domain별 이미지 갯수
  • I : source domain 갯수

• worst-case neighbor parameter space로 RRM (Robust Risk Minimization) 정의

  

  • $\gamma$: neightborhood of $\theta$를 정의하는 radius

  • 가령, sharp minima인 경우, “radius”가 $\gamma$보다 작게 되면 RRM이 커지므로, minima가 아니게됨

    

• Target domain Risk 와 ERM의 관계

  

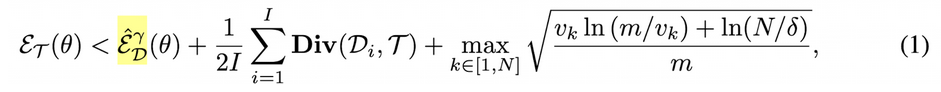
  • 1째항 : Source domain에서의 RRM
  • 2째항 : Target domain과 Source domain 분포의 간극
    • 
  • 3째항 : gamma와 sample 갯수에 연관된 confidence bound
    • delta : (표준확률정규분포 같은 느낌) 95% 확률과 오차분포로 정확하다 이런 의미인듯.
    • diam : minima랑 neightbor minima 간의 간극 중 가장 큰 것 (diameter)
    • vk : VC dimension (파라미터의 학습 가능한 volume. Vapnik–Chervonenkis dimension)

• Generalization gap := RRM - ERM으로 정의

  

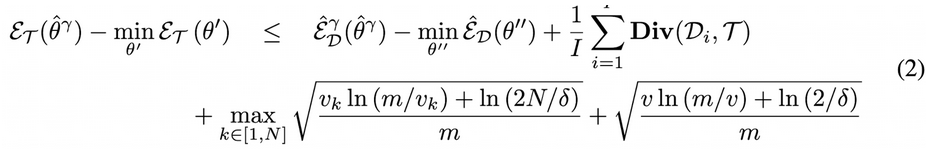
  • 1째항 : Source domain에서 RRM - ERM
  • 2째항 : Target domain과 Source domain 분포의 간극
  • 3째항 : Confidence bound

3. SWAD: Domain Generalization by Seeking Flat Minima

• Baseline : SWA

  • K epoch마다 weight를 모아서 update → Too sparse!

  

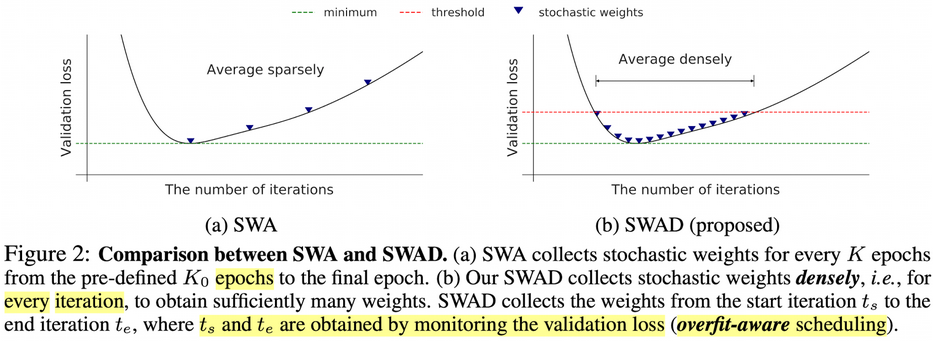
• SWAD

  • iteration마다 weight를 모아서 update → Dense!

  • Validation loss를 기준으로 start, end구간 정의

    • start ($t_s)$

      

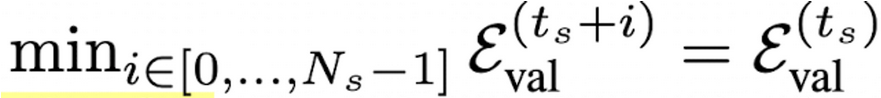
    • end($t_e)$

      

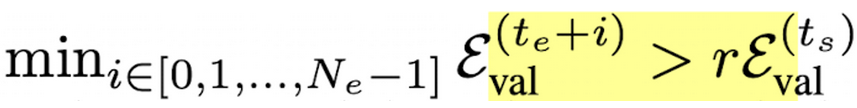
      • r : tolerance rate

• Local Flatness

  • RRM - ERM 대신 E(ERM) - ERM으로 정의 → RRM - ERM 정의하면 biased되어 있기 때문
  • MC Sampling을 100번 수행해서 $\theta’$을 구함

  

  

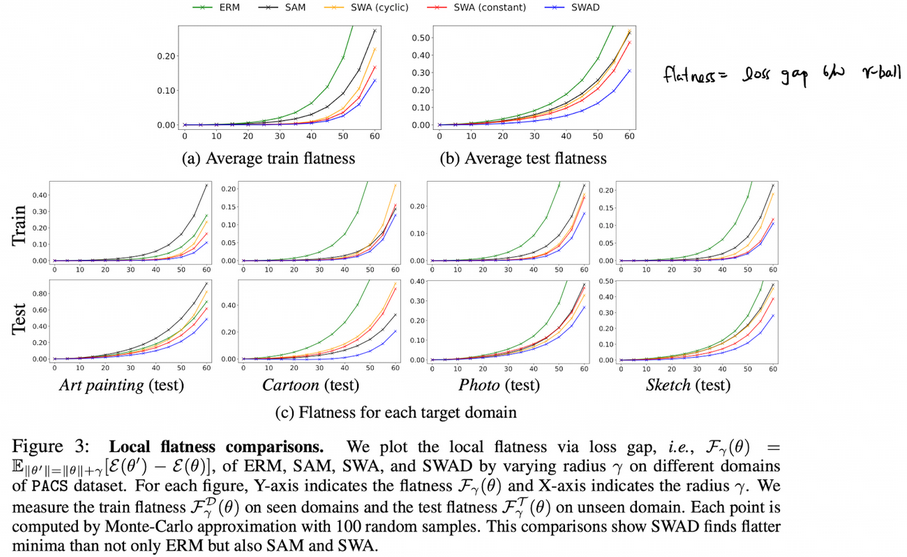
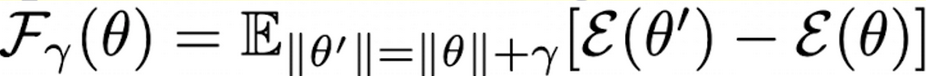
• Local Surface Visualization

  • ERM은 Train Loss의 flat loss 변두리에 위치하지만, SWAD는 Train/Test loss의 중간에 위치 (평균)
    • 각 점은 2.5K, 3.5K, 4.5K step의 weight가 계산한 loss
    • x axis : $\theta_2 - \theta_1$

    • y axis : $\frac{(\theta_3-\theta_1)-<\theta_3-\theta_1, \theta_2-\theta_1>}{

      \theta_2-\theta_1

      ^2 (\theta_2-\theta_1)}$

    • value : loss 값

  

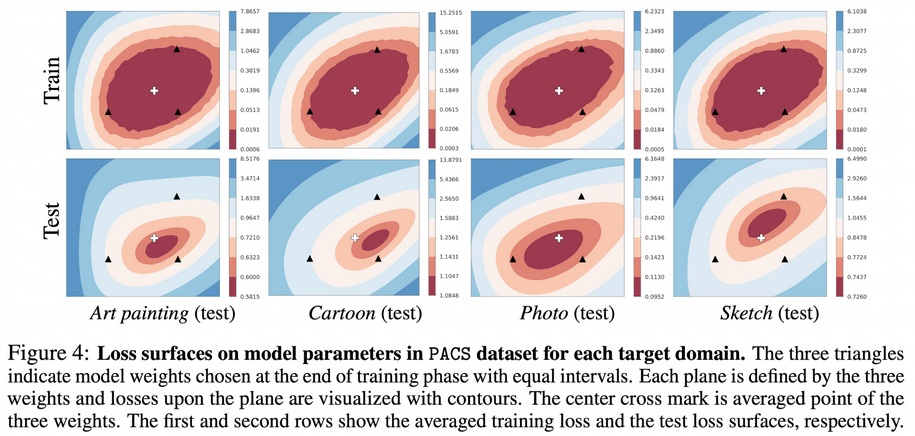
  • ERM은 모델 선택에 따른 accuracy가 요동치지만, SWAD는 overfit-aware scehudling으로 모델 selection-free

  

4. Experiments

Dataset

• PACS (9,991 images, 7 classes, 4 domains)
• VLCS (10,729 images, 5 classes, 4 domains)
• OfficeHome (15,588 images, 65 classes, 4 domains)
• TerraIncognita (24,788 images, 10 classes, 4 domains)
• DomainNet ( 586,575 images, 345 classes, 6 domains)

Results

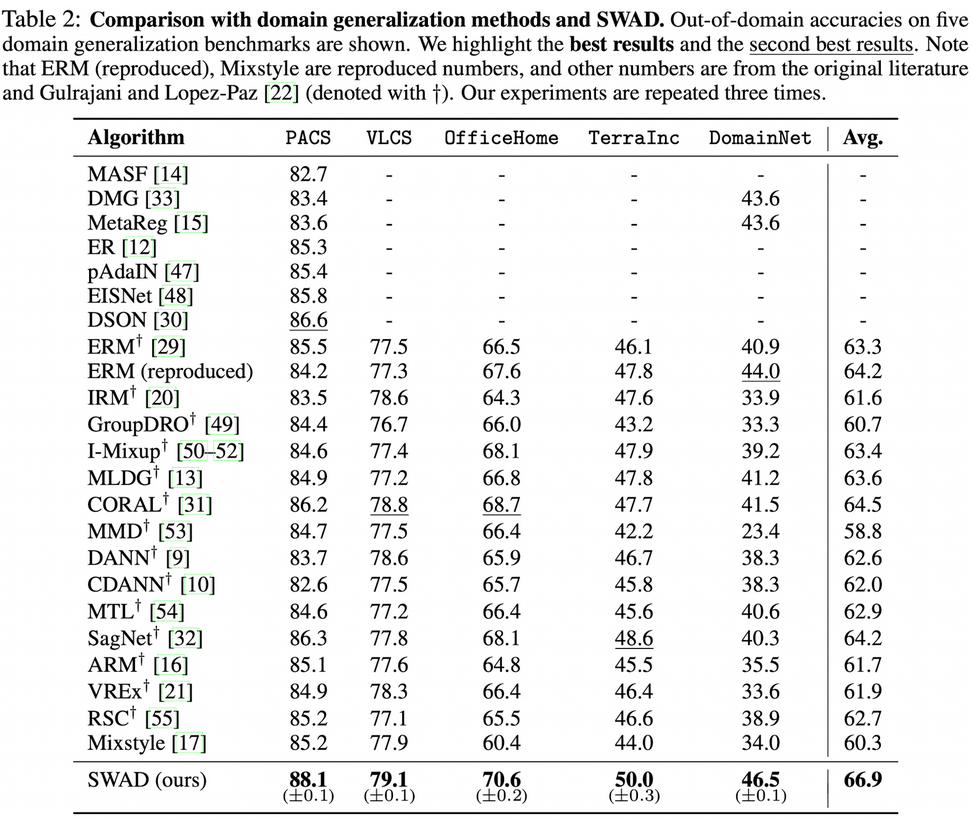
• Orthogonality

  

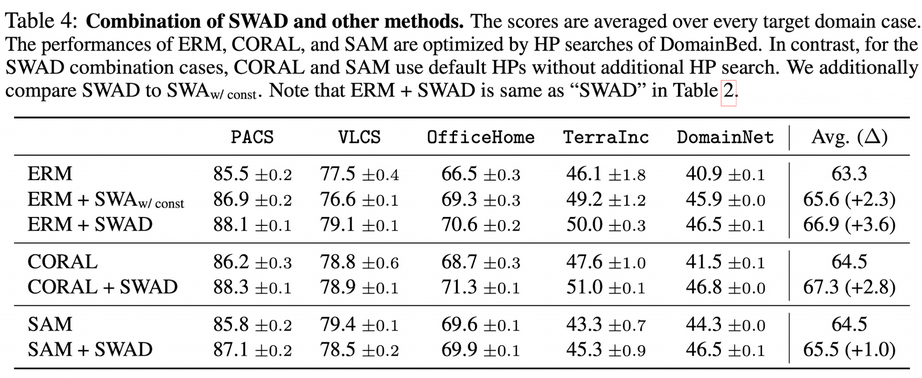
  • 기존 SOTA에 SWAD를 추가하면 모두 상승함

• In-domain / Out-of-domain

  

  • 기존 다른 DG방법들은 ID에서는 잘되나, OOD에서는 잘 안됨 (SWA, SWAD 제외)

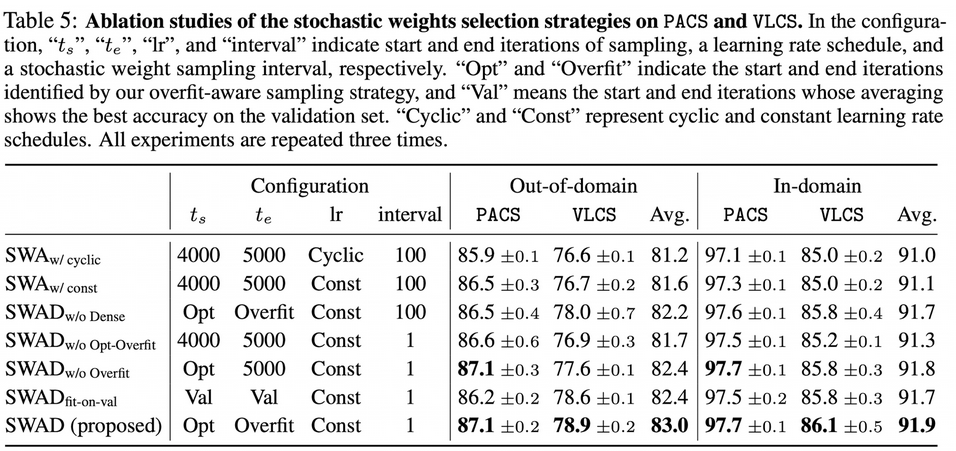
Ablation study

Imagenet Robustness

• BGC : bg/fg 영역을 수정해도 모델이 consistent한 값을 예측하는지 확인 (robustness)
• ImageNet-C (mCE) : mean corruption Error. Gaussian Blur, 등 corruption에 따른 error가 적은지 체크 (robustness)
• ImageNet-R : accuracy. (DG)

5. Conclusion

• DG는 Flat minima를 찾음으로써 실현 가능하다.
• Flat minima를 찾는 것이 DG를 푸는 것임을 이론적/실험적으로 증명했다.
• Mixup, Cutmix등 기존 augmentation기법은 OOD (DG)의 성능을 해친다.