[B-Rep Generation] HoLa: B-Rep Generation using a Holistic Latent Representation
[B-Rep Generation] HoLa: B-Rep Generation using a Holistic Latent Representation
- paper: https://arxiv.org/pdf/2504.14257
- github: X
- ACM TOG 2025 & SIGGRAPH 2025 accpeted (인용수: 2회, ‘25-09-27 기준)
- Downstream task: 3D CAD B-REP (Boundary Representation)을 생성하는 task (Conditional / Unconditional)
1. Motivation
-
기존 연구들에서는 3D 물체의 표면, 경계 곡선, 그리고 topological 관계를 서로 다른 표현공간 (representation space) encoding하여 학습하였음.
- 한계점
- 명시적인 (Explicit) topological 제약이 없었기에 표면 $\to$ 곡선 multi step으로 생성 할 때 error accumulation 발생
$\to$ 인접하는 표면간에 접선이 경계곡선으로 표현되는 사전 지식 (inductive bias)를 바탕으로, 통합된 표현공간으로 encoding해보면 어떨까?
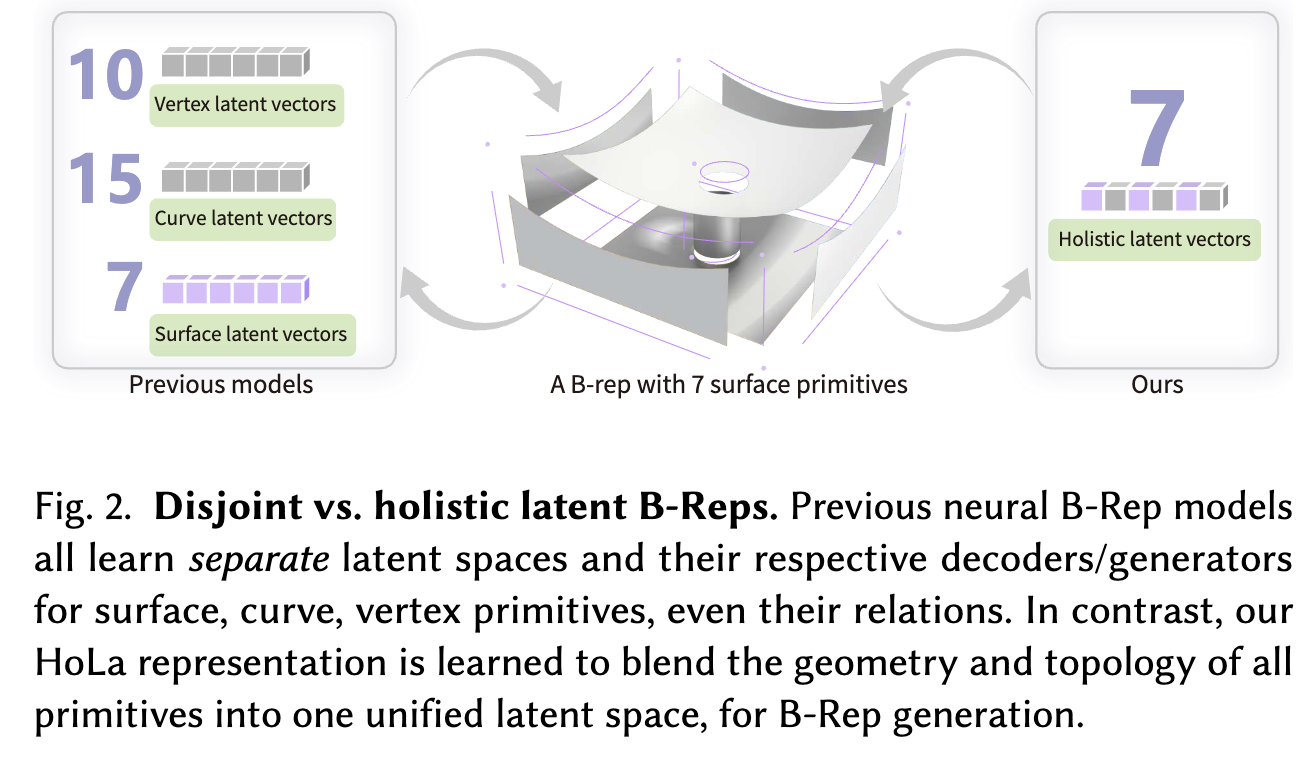
- 한계점
2. Contribution
-
3차원 표면 pair 간의 연결성을 (intersection) module을 통해 연결유무를 파악하고, 표면 & 곡선 정보를 통합된 latent로부터 복원하는 Holistic Latent (HoLa)를 제안함.
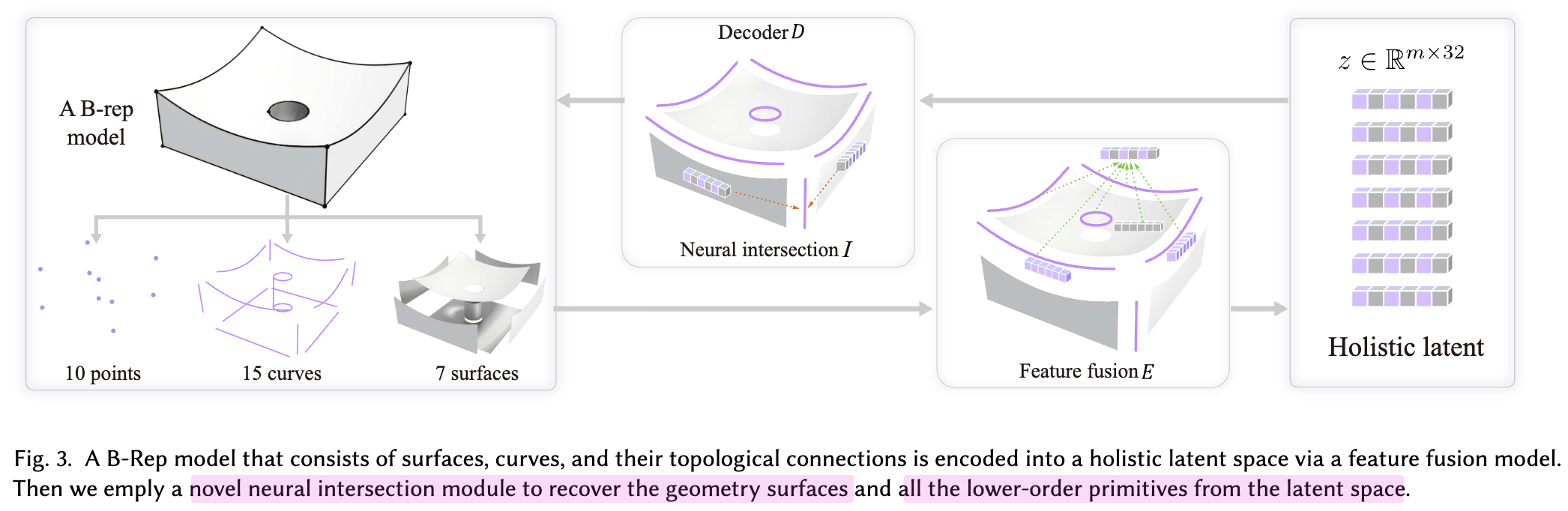
- VAE (conv + self-attention + cross-attention)
- input: curves / surfaces
- output: latent vector $z$
- Latent Diffusion Model (LDM)
- input
- condition vector ($c \in R^{256}$)
- latent vector $z$
- output
- curves
- surfaces
- input
- VAE (conv + self-attention + cross-attention)
3. HoLa
Overview
- CAD Model
- $S$: Surface. ${S_i}_{i=1}^m$
- B-Spline로 표현하며, uniform sampling을 통해 ($16\times16\times3$)로 정의
- $C$: Curve. ${C_i}_{i=1}^n$
- B-Spline로 표현하며, uniform sampling을 통해 ($16\times3$)로 정의
- $V$: Vertices. ${V_k}_{k=1}^l$
- $T_{SC}$: Surface-to-Curve connections $\in {0, 1}, R^{m \times n}$
- ${V, T_{sc}}$를 통해 Vertice를 curve에 묶어서 표현
- $T_{CV}$: Curve-to-Vertices connections $\in {0, 1}, R^{n \times l}$
- $S$: Surface. ${S_i}_{i=1}^m$
-
VAE Training
-
encoder
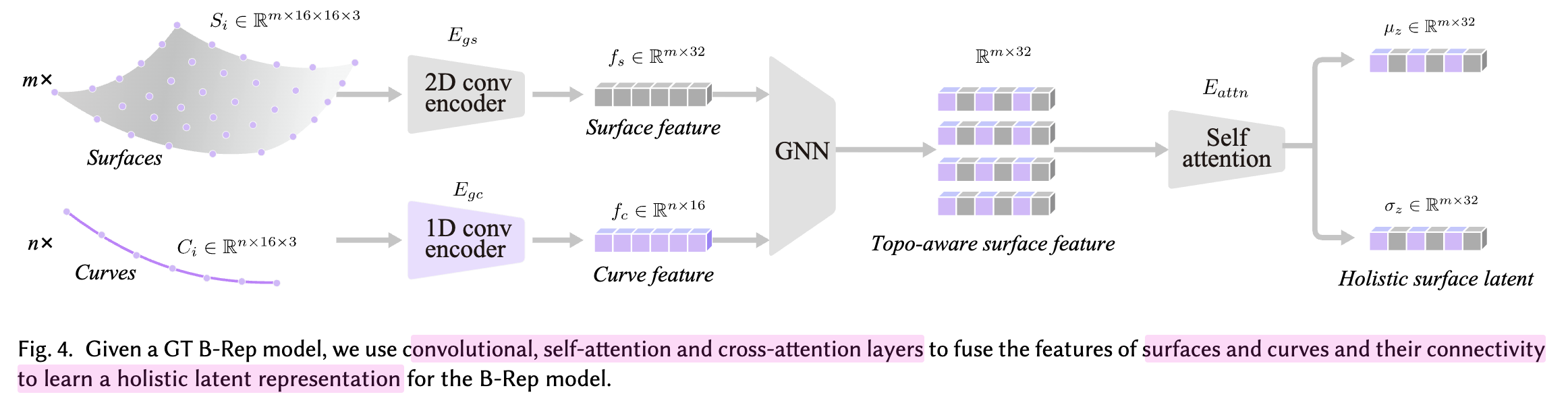
-
input: ${S,C,T_{SC}}$
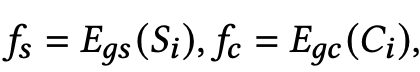
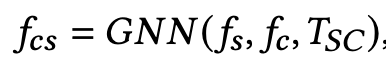
- Downsample + CNN: $S \in R^{m \times 16 \times 16 \times 3} \to R^{m \times 32}$
- Downsample + CNN: $C \in R^{n \times 16 \times 3} \to R^{n \times 16}$
- GNN: $(R^{m \times 32}, R^{n \times 16}, {0,1}^{m \times n}) \to T_{SC} \in R^{m \times n}$: curve-aware feature vector ($f_{sc}$)
- Self-attention layer: $R^{m \times n} \to R^{m \times n}$
- MLP layer: $E_{mlp}: R^{m \times n} \to (R^{m \times n}, R^{m \times n})$
-
output: $z_s \in R^{m \times (2\times2\times d)}$
- m: surface별 embedding
- 2: spatial resolution
- 2: direction
- d = 8 : feature dimension
-
-
decoder:
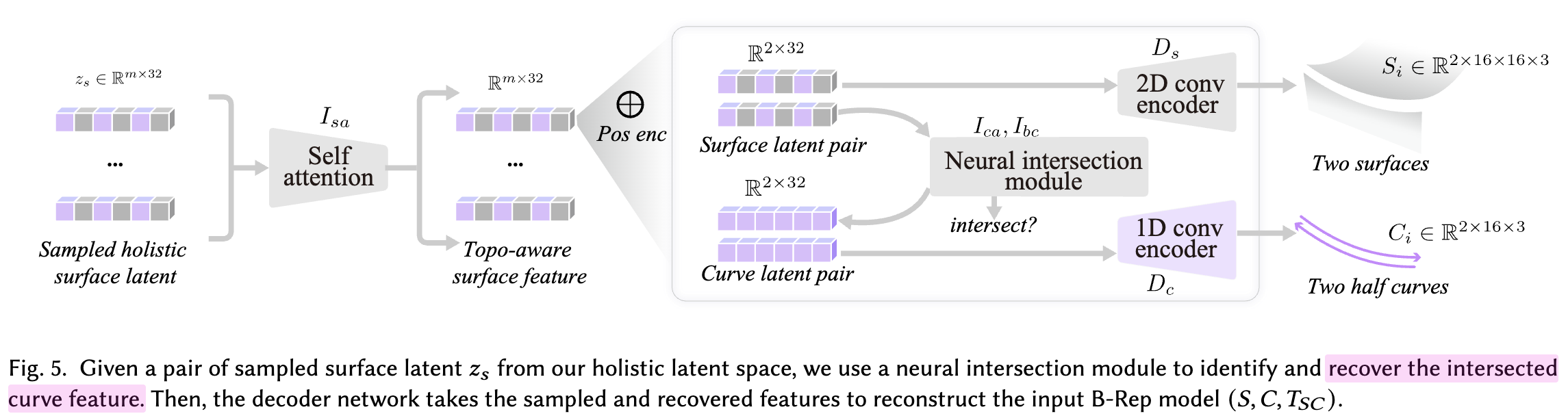
-
input: : $z_s \in R^{m \times (2\times2\times d)}$
-
intersection Module $\mathbb{I}: R^{(m \times 32, m \times 32)} \to (R^{16}, {0,1})$
- curves, vertices 를 latent space에 반영하게 하기 위해 사용
- Self-attention + cross-attention + MLP 통과
- self-attention: $R^{32} \to R^{32}$
- cross-attention: $(R^{32}, R^{32}) \to R^{16}$
- mlp: $R^{16} \to R^{16}$
- binary classifier: $R^{16} \to {0,1}$
- surface가 몇번째인지 positional encoding 정보 추가
- Self-attention + cross-attention + MLP 통과
- input: m개의 surface latent 쌍
- output: 두 surface가 접하는지 (1) 아닌지 (0) 예측
- curves, vertices 를 latent space에 반영하게 하기 위해 사용
-
output: ${S,C,T_{SC}}$
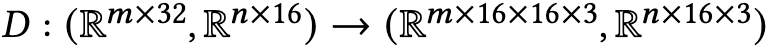
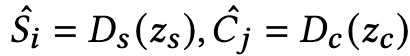
-
-
-
LDM Training
- input
- Conditions: $c \in R^{256}$
- Latent embedding $z_s \in R^{m \times (2\times2\times d)}$
- Output: ${S,C,T_{SC}}$
- input
-
Loss
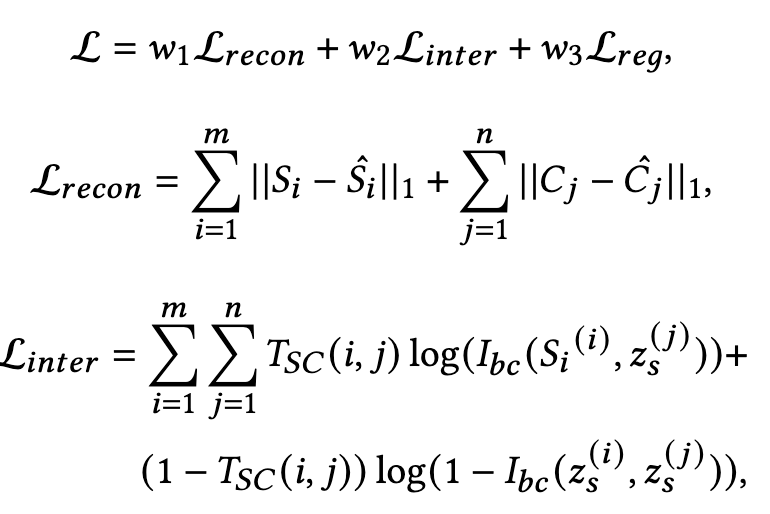
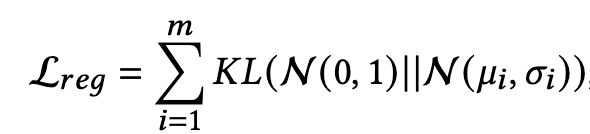
-
Half-Curvature
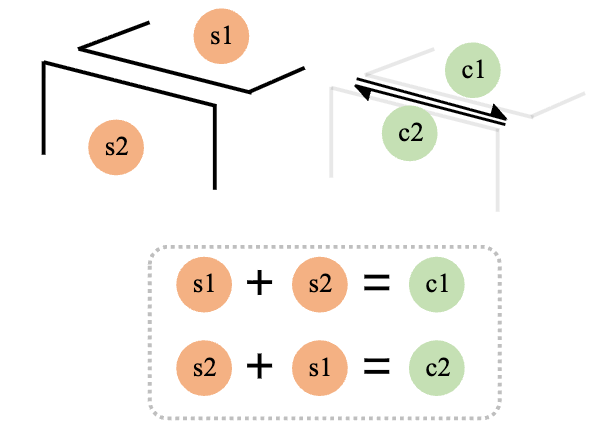
- $16 \times 3$로 curve를 uniform sampling하는 과정에서 curve의 방향이 고정되어, 임의로 방향이 지정됨 $\to$ 이는 학습을 robust하지 못하게 함
- L1 loss대신 Chamfer distance 을 적용 (inner hole: clock-wise loop, outer hole: counter-clock wise)
-
(Conditional) Generation
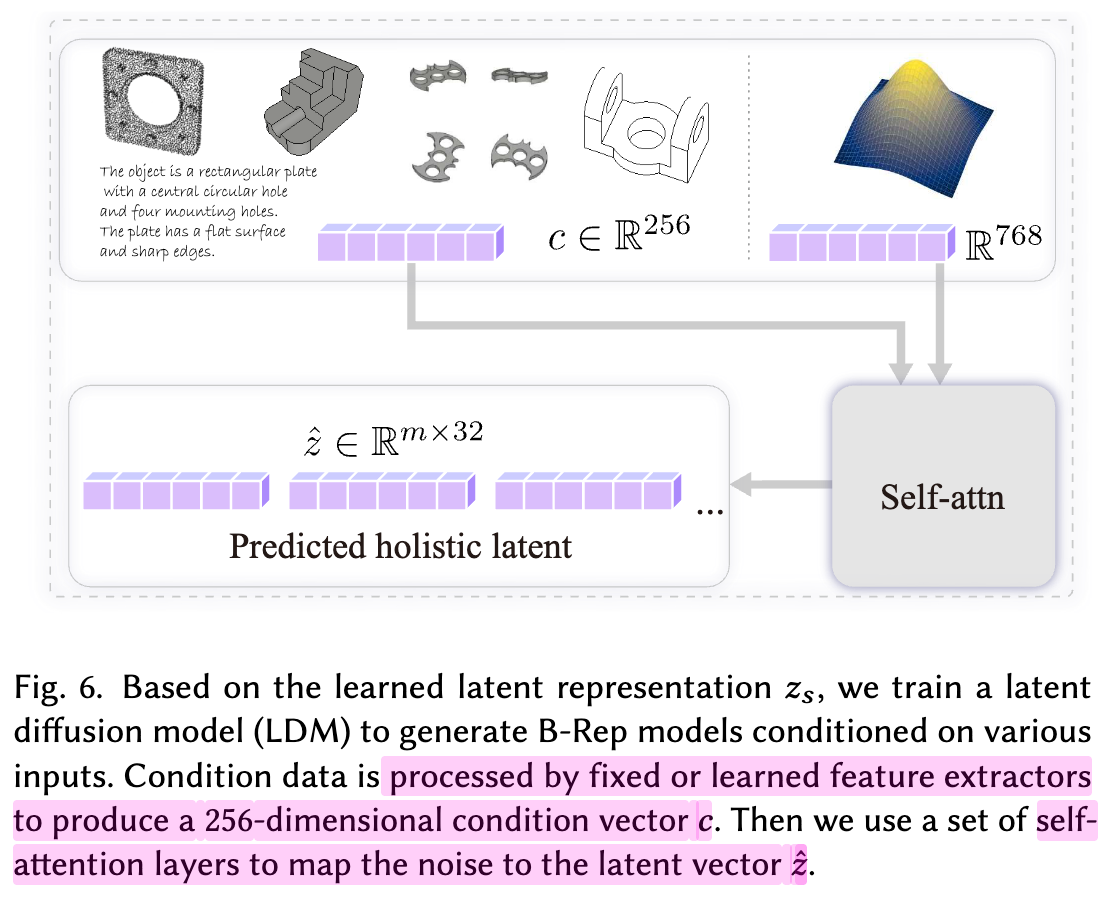
-
condition을 latent와 함께 부여하여 복원
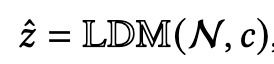
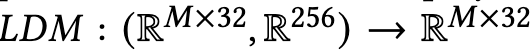
- image: dinov2 embedding (1024d) $\to$ MLP (256d)
- 학습할 때 freeze
- point clouds: PointNet
- 학습할때 unfreeze
- image: dinov2 embedding (1024d) $\to$ MLP (256d)
-
-
Post-process
- Intersection module + Decoder 통과 후, embedding은 BSpline을 통해 sample points를 surface, curves로 복원
4. Experiments
- Dataset
- DeepCAD dataset
- 7 ~ 30 surfaces를 갖는 models만 활용
- Train: 47,284
- val: 3,517
- test: 2,424
- 7 ~ 30 surfaces를 갖는 models만 활용
- DeepCAD dataset
- Evaluation Metrics
- Validity ($\uparrow$): 전체 생성된 samples중 유효한 samples의 비율
- Average Light Field Distance (LFD) ($\uparrow$): light field distance를 기반으로 생성된 sample의 “novelty”를 평가함. 얼마나 training set 기준 overfitting이 덜되었는지 평가
- Coverage ($\uparrow$): 생성된 samples로 cover되는 test-set의 비율. Chamfer Distance (CD)기반으로 closest neighbor를 선정
- Jensen-Shannon Divergence (JSD) ($\downarrow$): 생성된 samples와 test set의 분포 차이 ($28^3$ voxel point cloud로 표현)
- Maximum-Mean Discrepancy (MMD) ($\downarrow$): 생성된 sample과 nearest neighbor로 mapping된 test-set의 평균 CD 거리
- Cyclomatic Complexity (CC) ($\uparrow$): 생성된 sample의 wireframe graph 표현 에 존재하는 loop의 수. 복잡도를 표현
- Mean curvature (MC) ($\uparrow$): 생성된 samples의 averaged mean curvature
-
정량적 결과
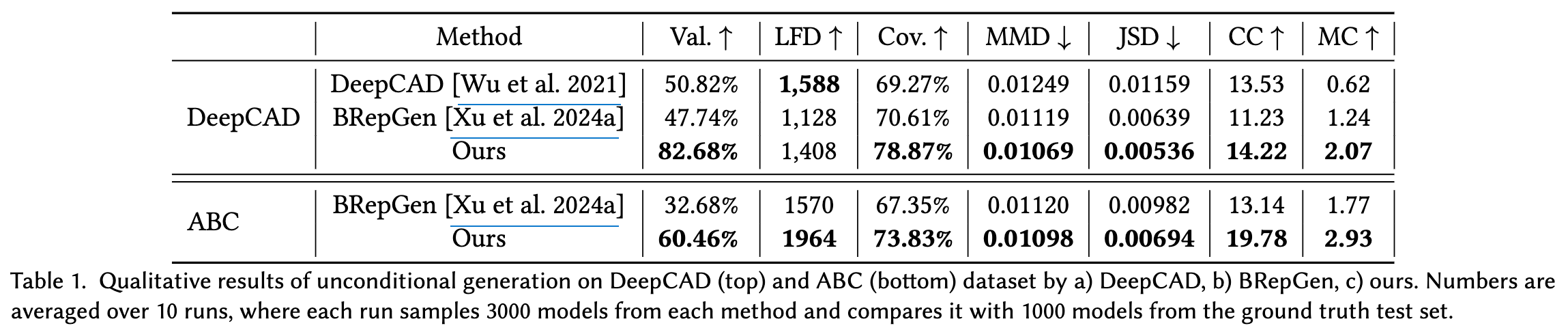
-
정성적 결과
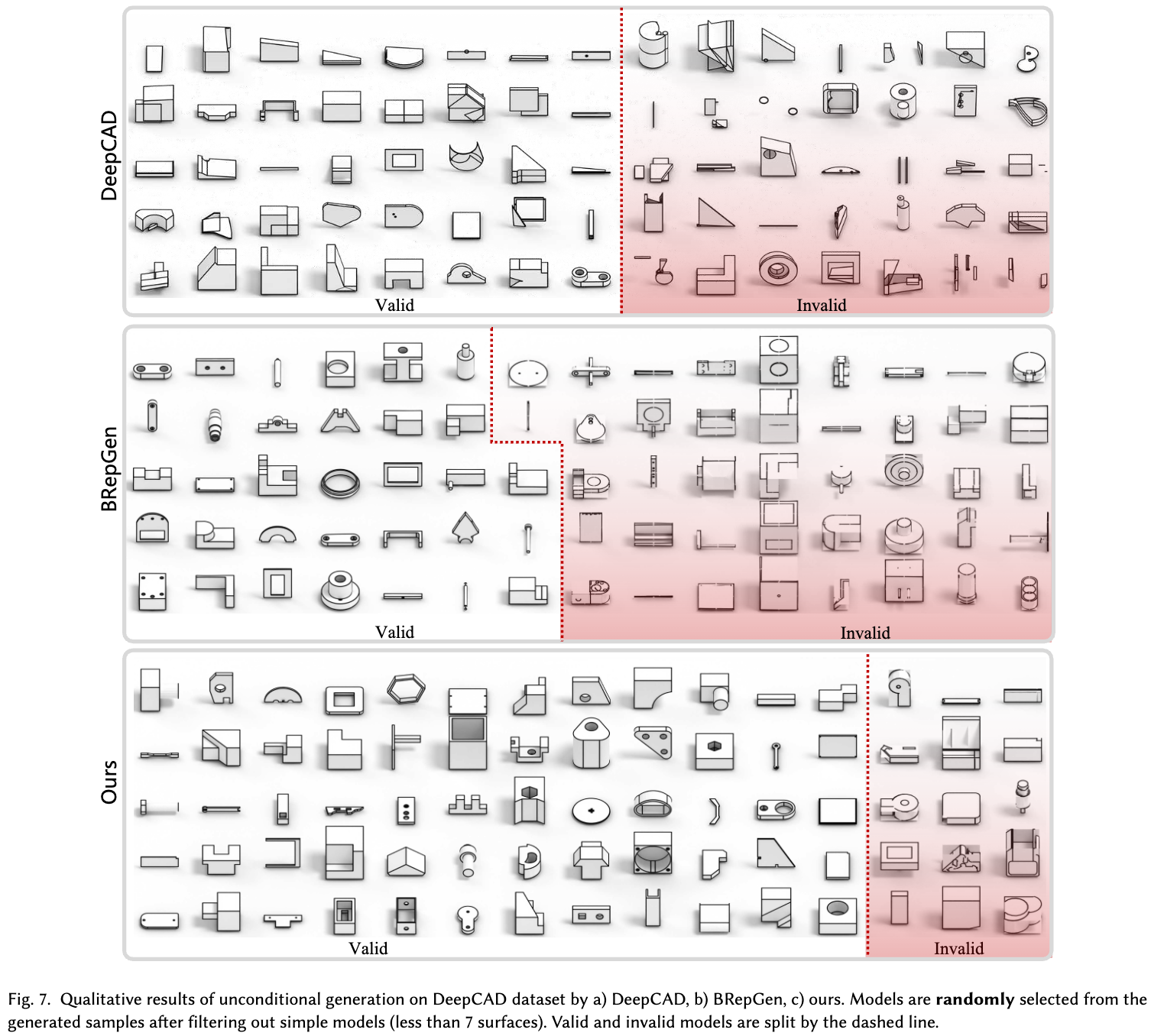
-
Unconditional Generation 결과

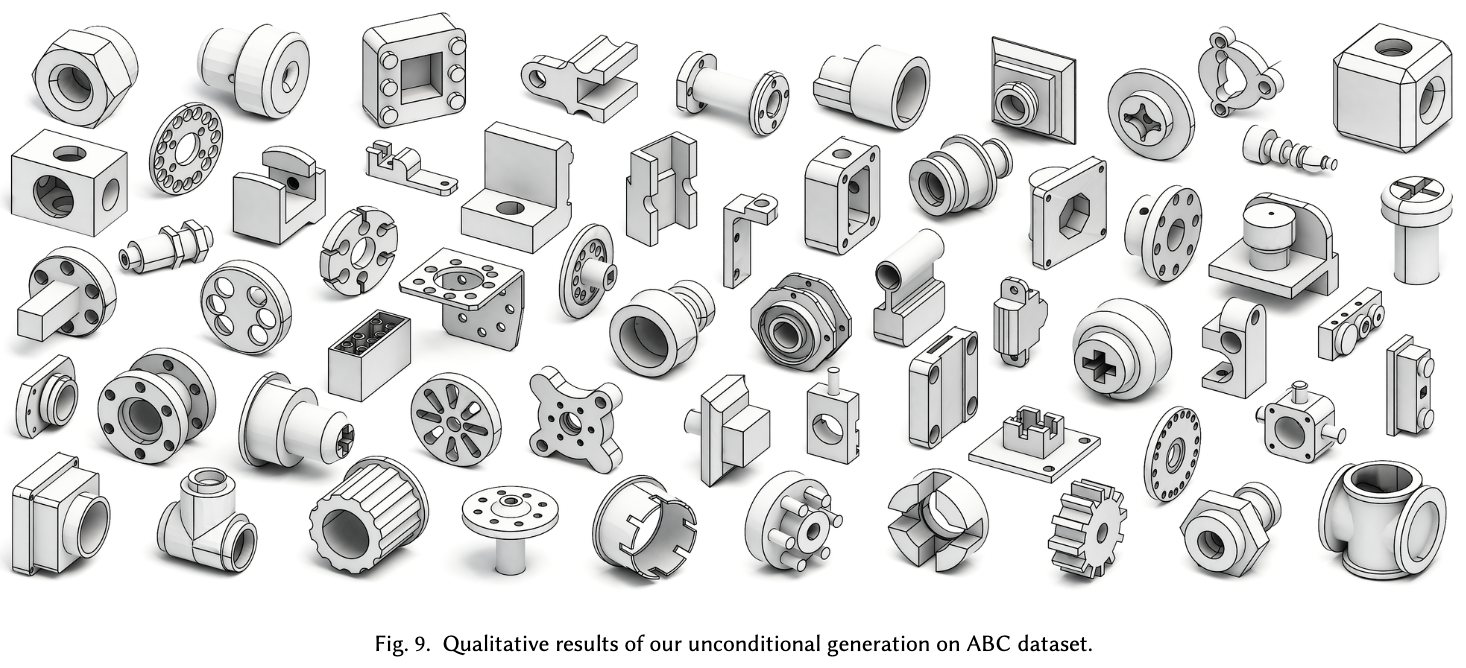
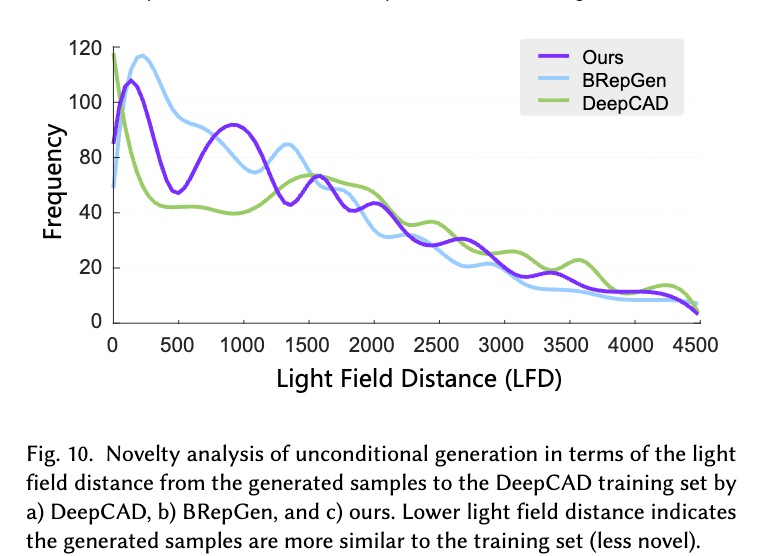
-
Conditional Generation
-
정량적 결과
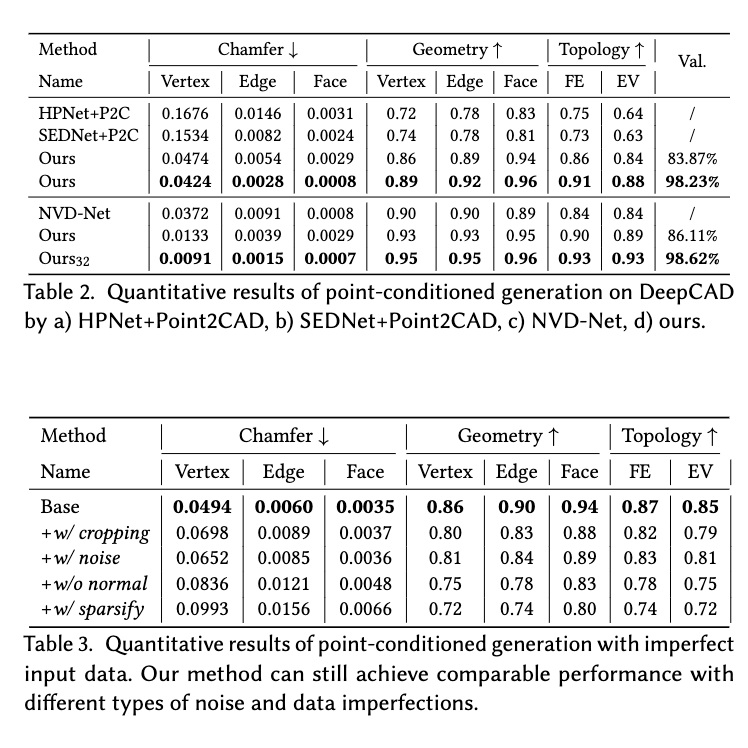
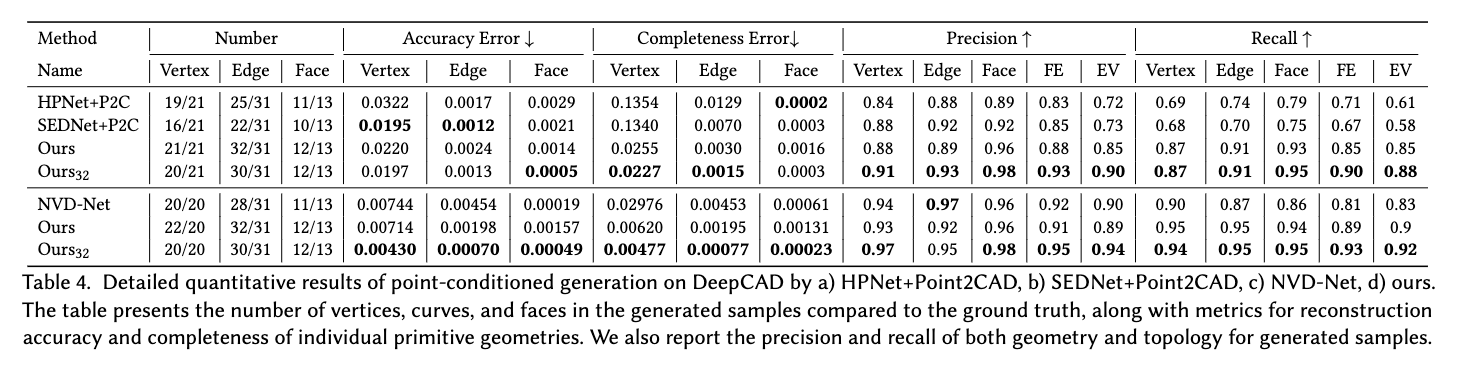
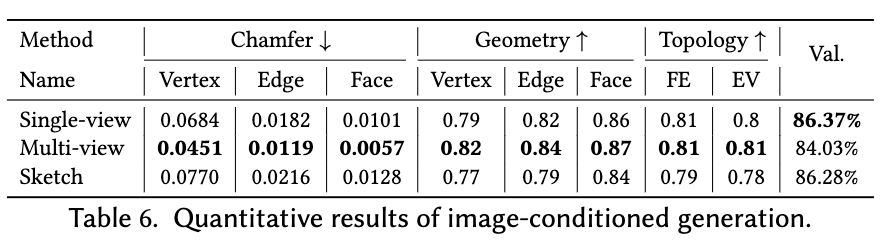
-
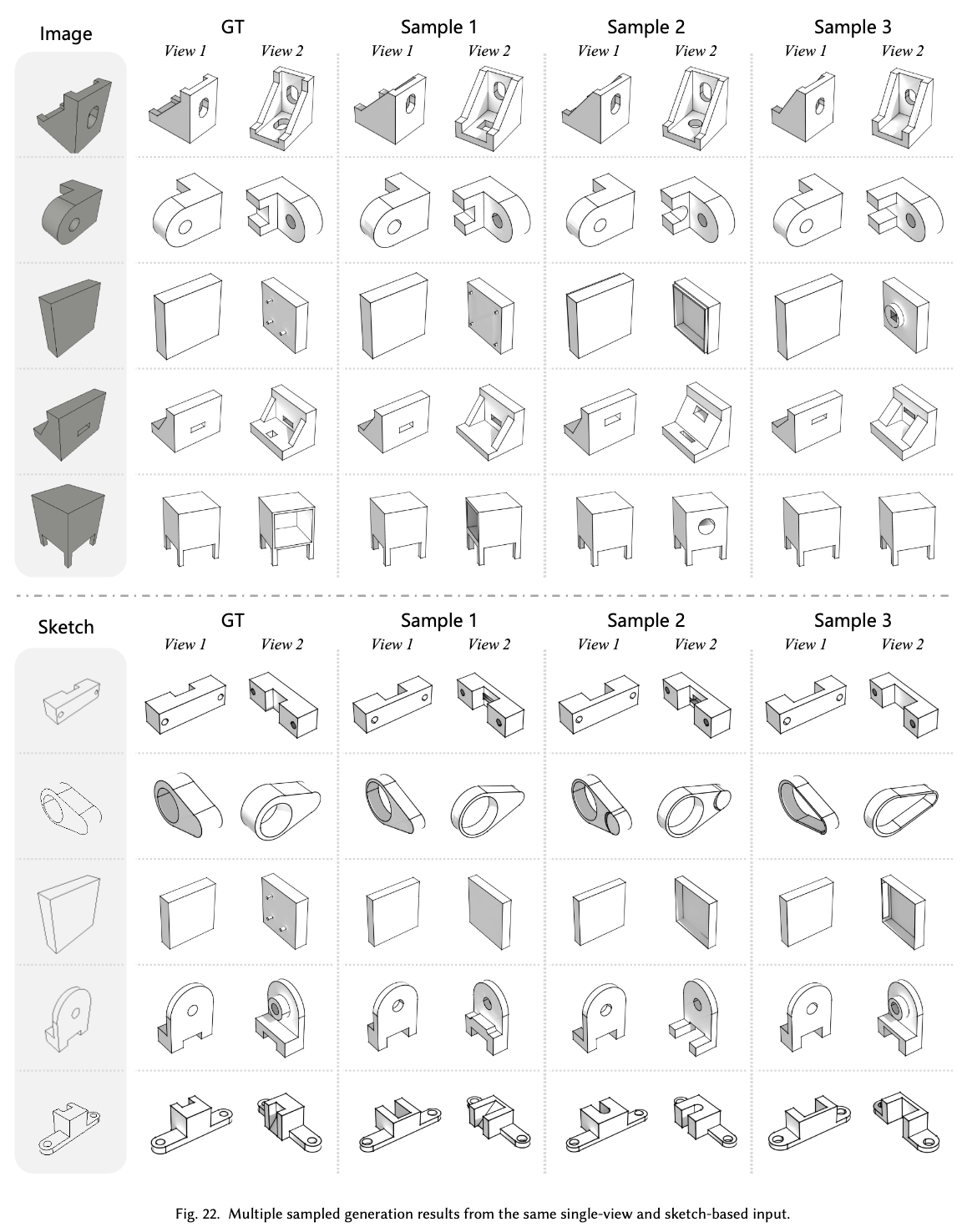
정성적 결과

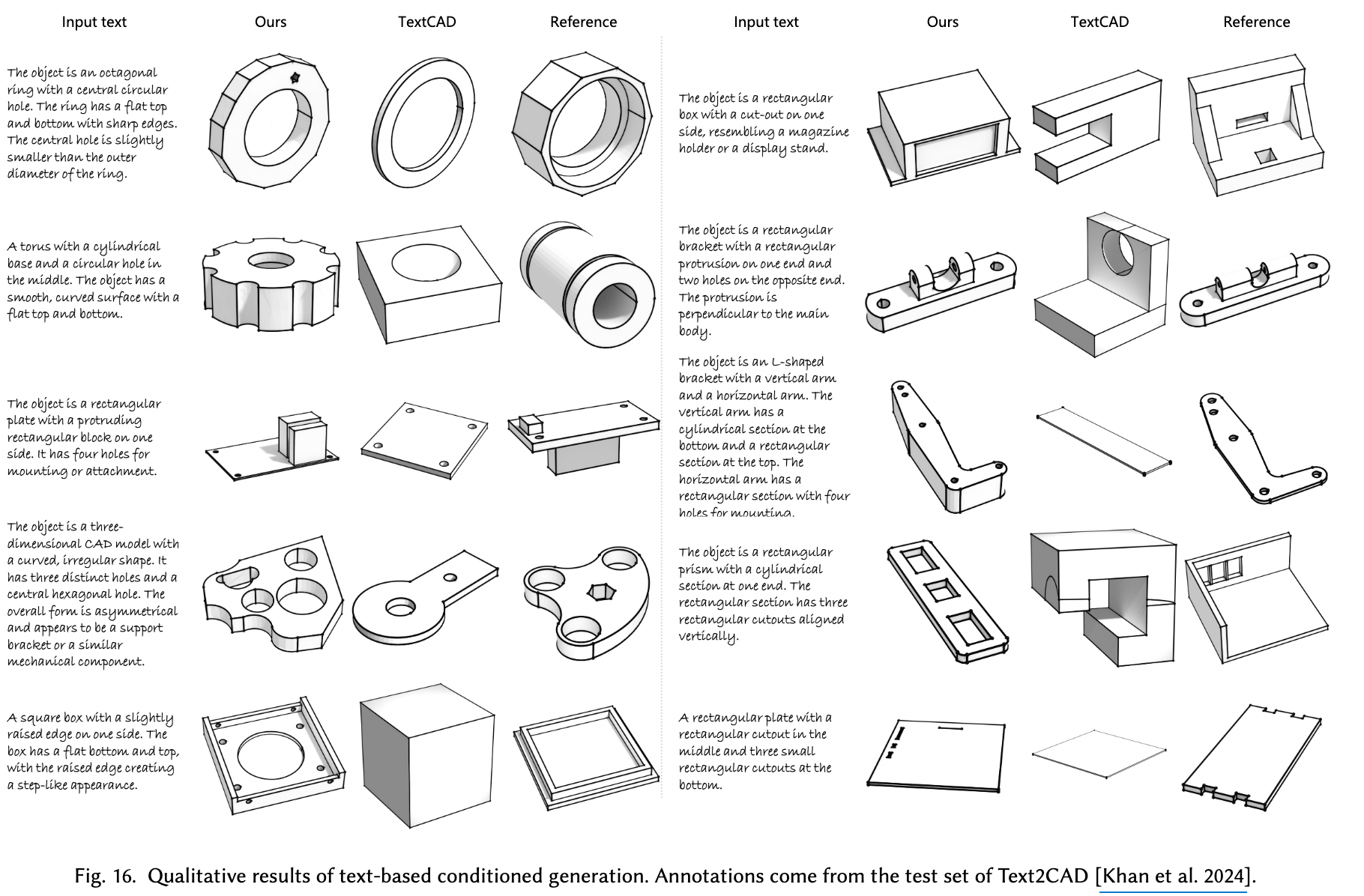




-
-
실패 사례
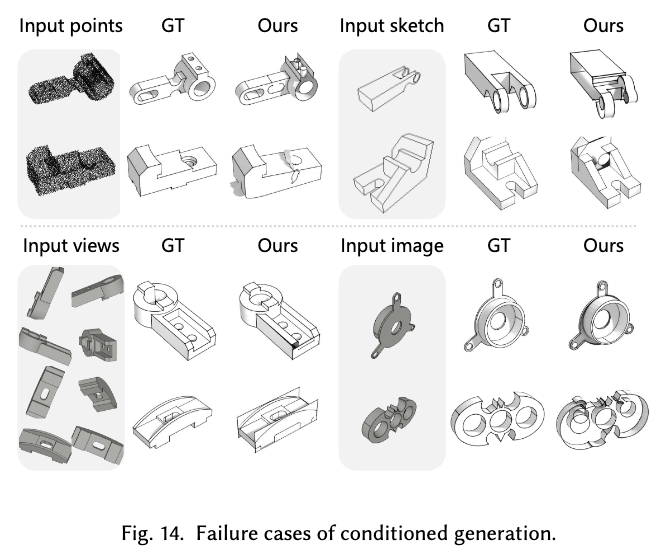
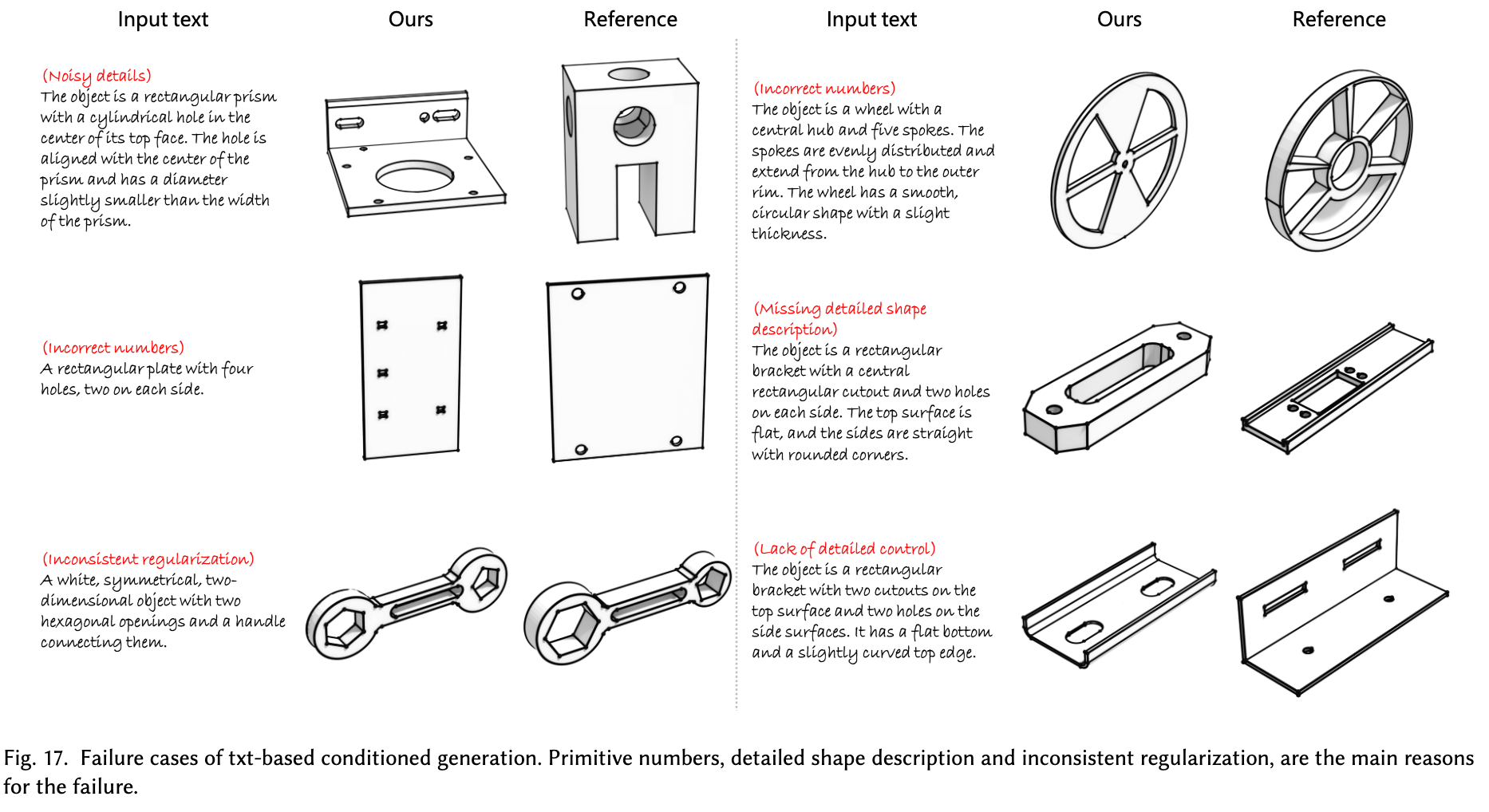
-
Out-of-Distribution 사례
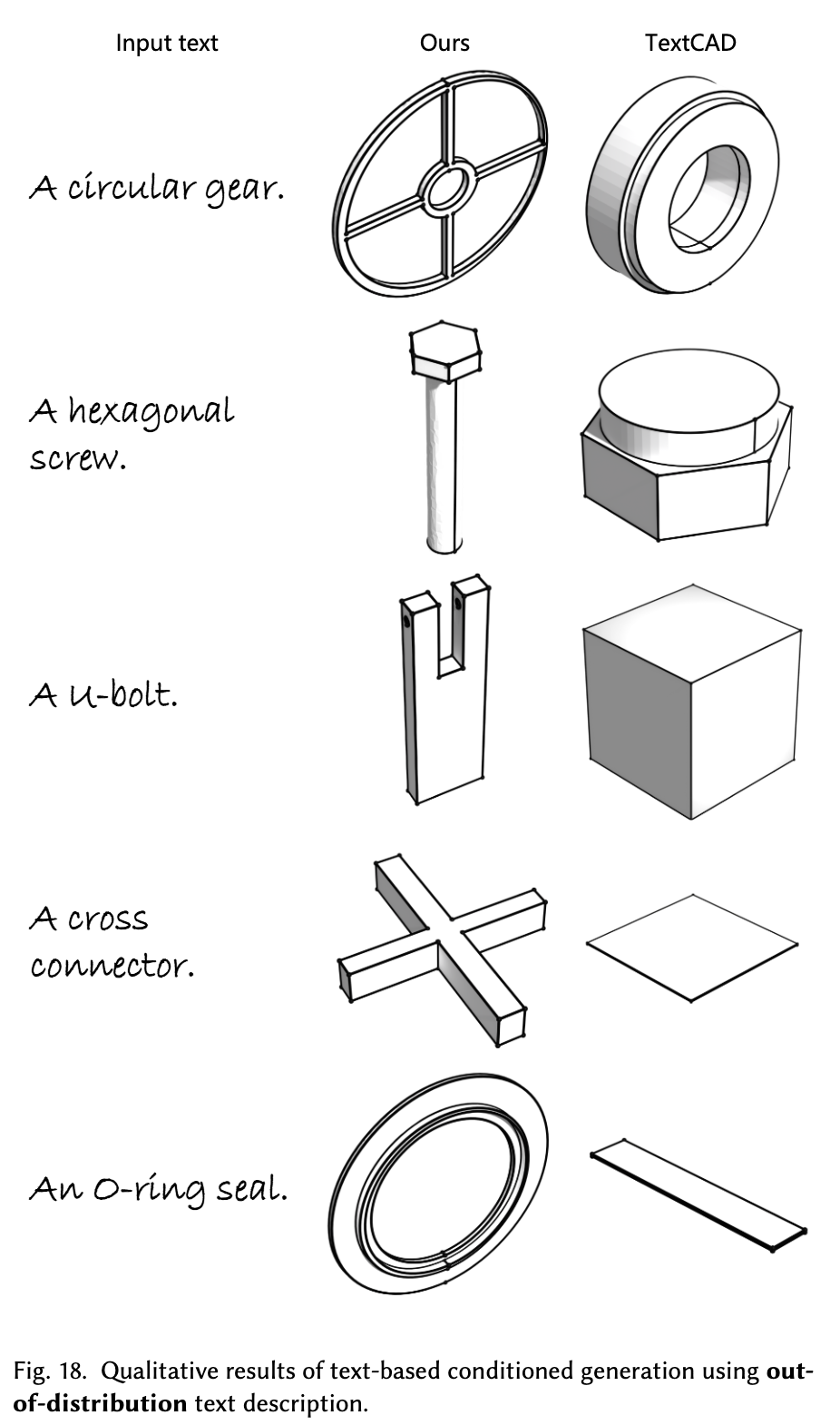
-
Ablation Studies
-
SA / SR / HE 유무에 따른 분석

-
반복 횟수에 따른 비교
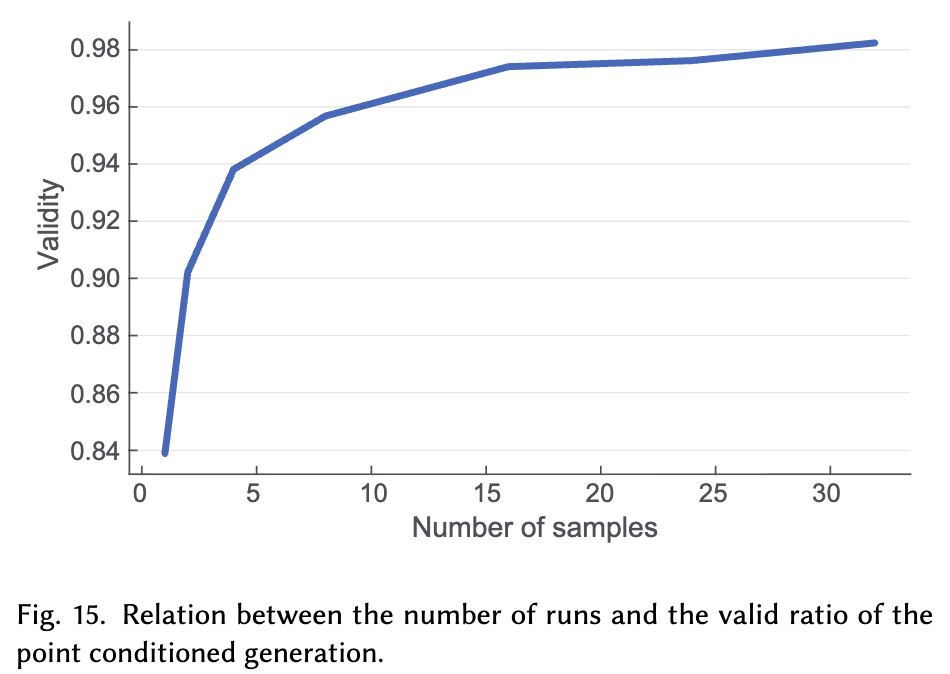
-