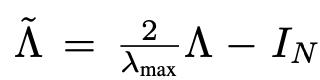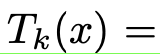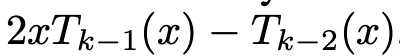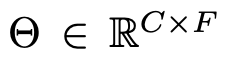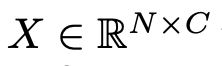[SSL] GCN: SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

[SSL] GCN: SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

• paper: https://arxiv.org/pdf/1609.02907.pdf
• github: https://github.com/tkipf/gcn
• ICLR 2017 accpeted (인용수: 31,192회 ‘24-02-15 기준)
• downstream task: Document classification for graph-based DB

1. Motivation

• graph-structured data를 효율적으로 처리하기 위한 Convolution Network의 효율적인 variant인 Graph-Convolution-Network가 필요함

2. Contribution

• Graph-structured data에 directly 적용 가능하고, layer-wise propagation이 가능한 graph-conv.-net을 제안함
  • 1st order approximation of spectral graph convolution에서 동기를 얻음
• semi-sup. classification에 어떻게 적용할 수 있는지 제안함

3. GCN

• propagation rule

  

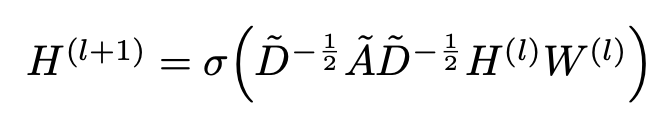
  • $\tilde{A}$: A+$I_N$
    • A: Adjacent matrix. $a_{ij}=1$ if i and j node has at least one edge connected
    • $I_N$: Identity matrix of shape N
  • $H^{(l)}$: l번째 layer의 activation matrix $\in \mathbb{R}^{N \times D}$
  • $W^{(l)}$: l번째 layer의 learnable weight matrix $\in \mathbb{R}^{N \times D}$

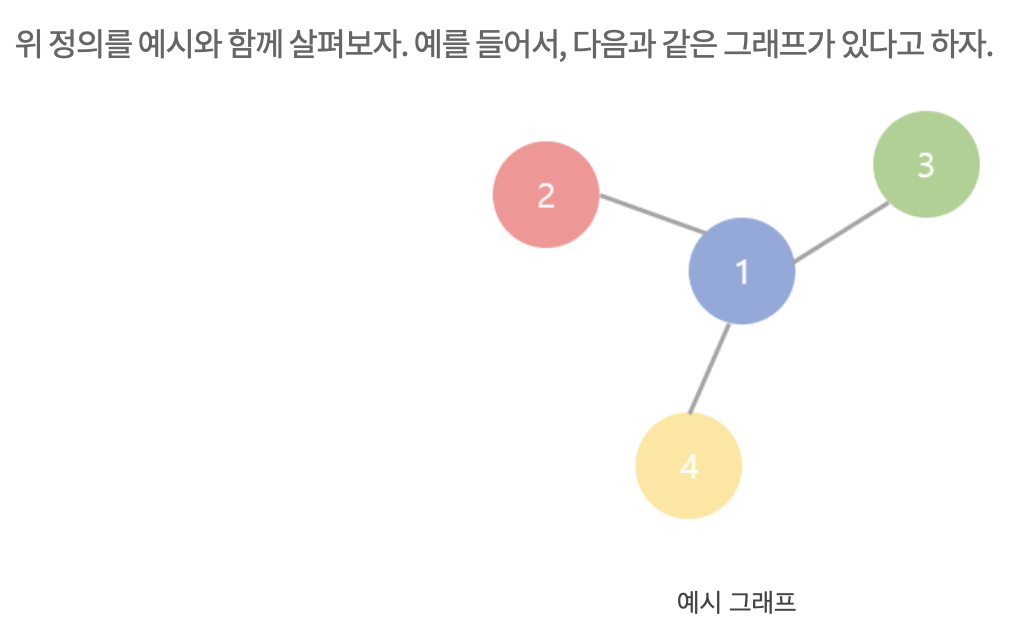
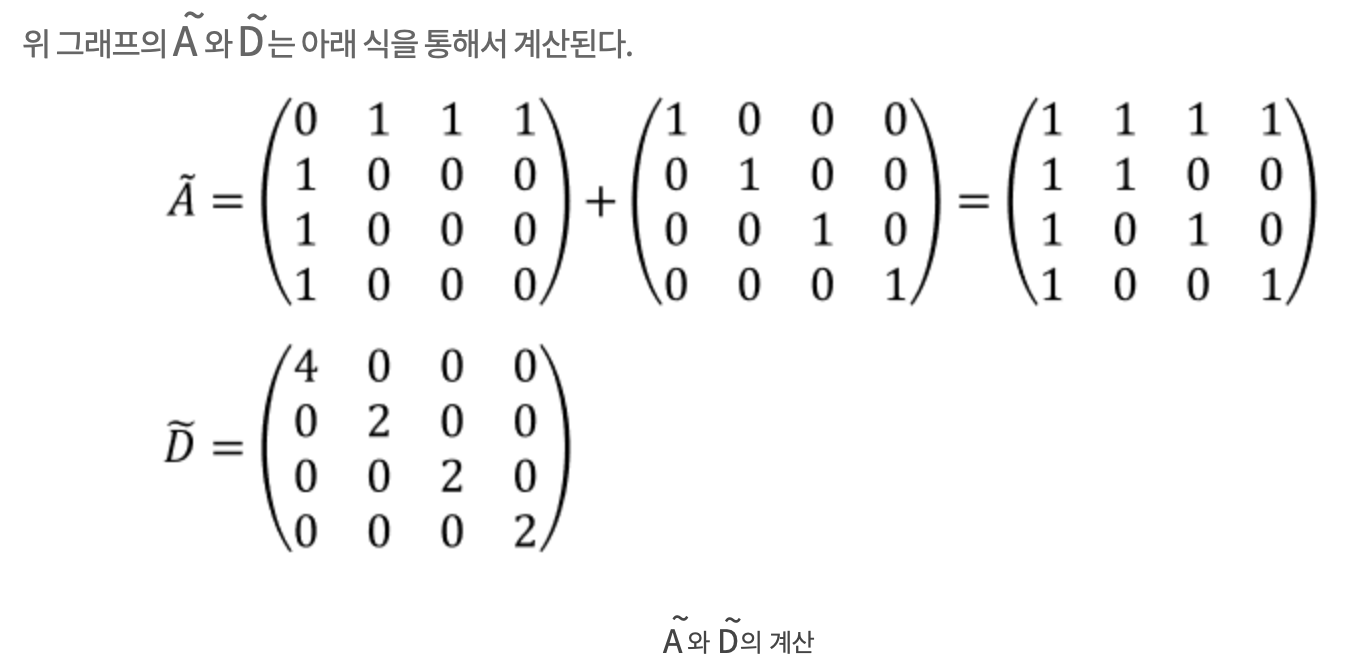
• reference: https://process-mining.tistory.com/176

• 위 식은 1st order approximation of localized spectral filters on graphs에 의해 motivated되었다고 함

• Spectral Graph Convolution

  • Fourier domain에서 signal x와 filter $g_{\theta}$간의 곱으로 표현

    

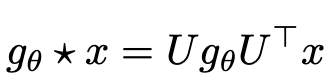
    • U: Normalized graph Laplacian L의 eigenvectors

      • $L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}$

    • egienvalue decomposition은 너무 계산량이 크므로 Chebyshev polynomials로 k번째 eigenvalue까지 turncate하면

      

      • 
      • 

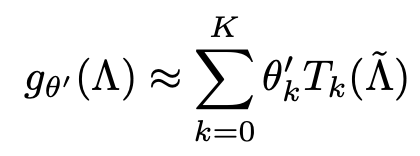
• $\tilde{\Gamma}$에서 $\lambda_{max}$를 2로 근사하여 linear formulation으로 근사하면

  

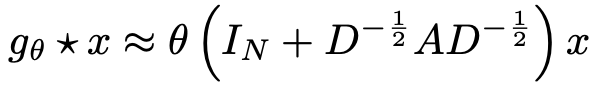
• 이를 일반화 하면

  

  • 
  • 
  • 

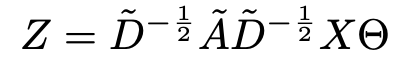
• Semi-superivesd Classification

  

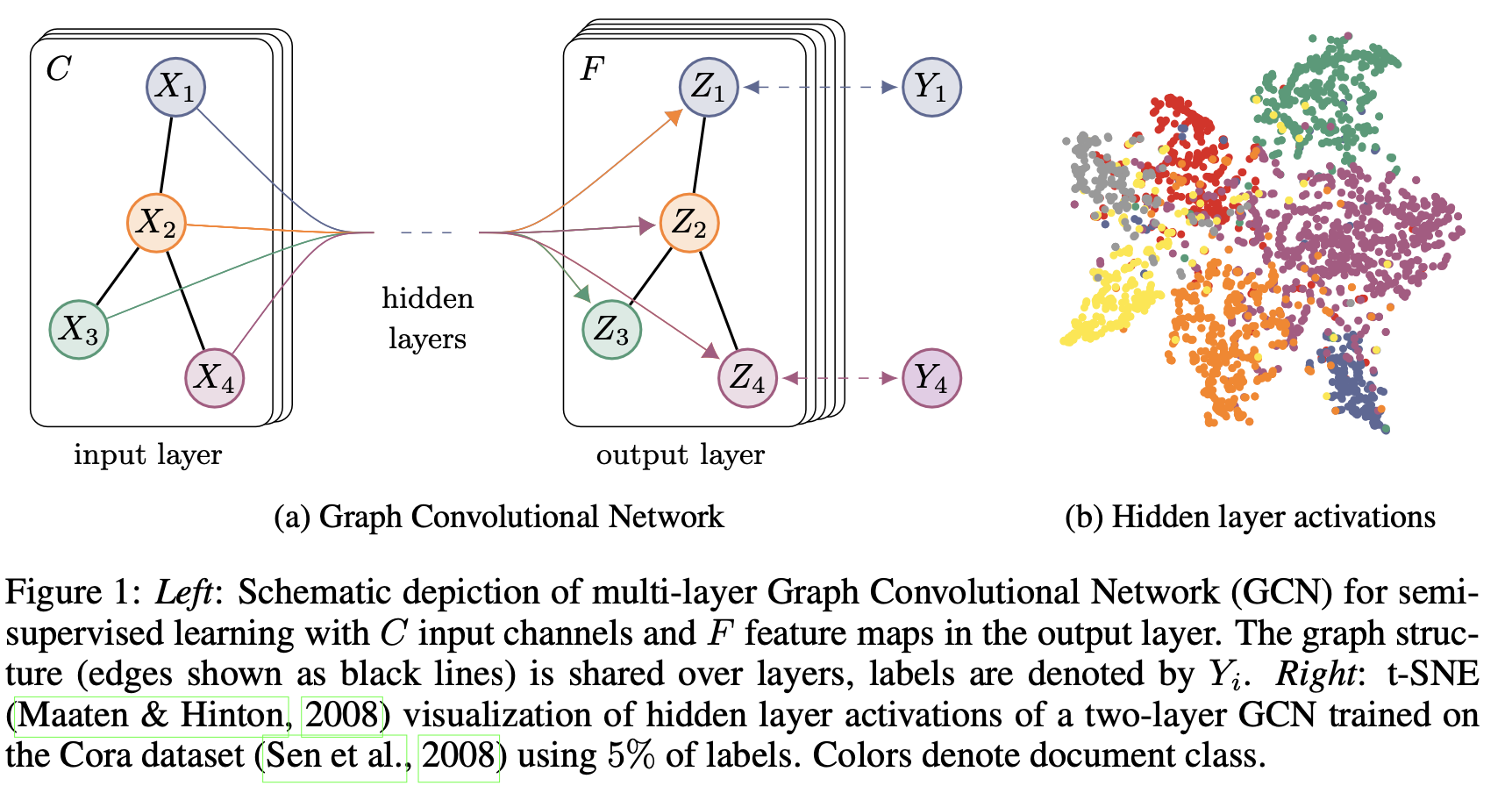
  • foward process of a model

    

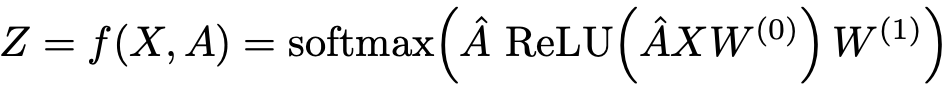
    • A: adjacency matrix. $a_{ij}=1$ if i and j node has edge.
    • 

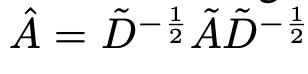
  • Loss

    

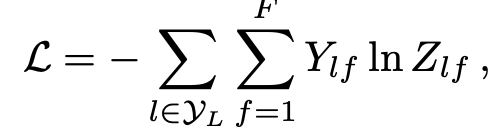
4. Experiments

• Dataset

  

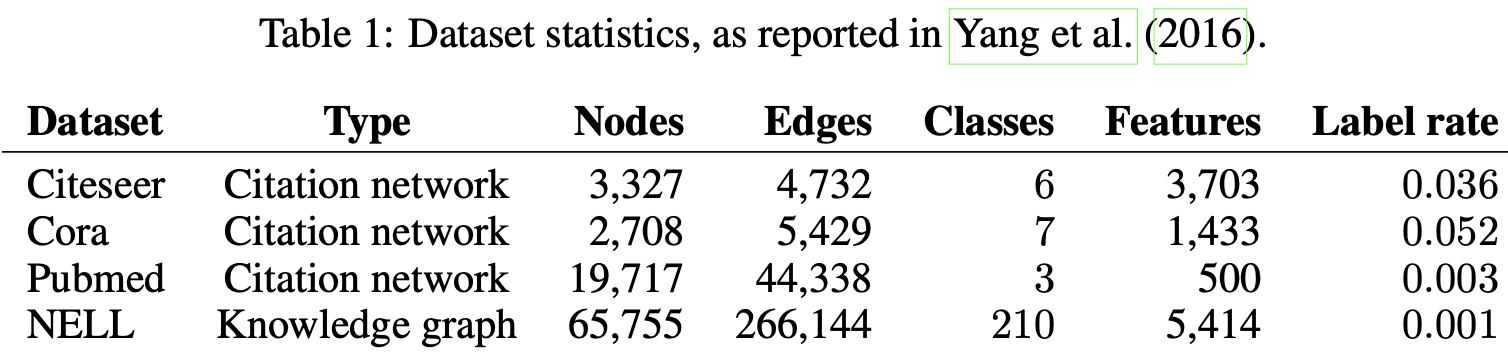
• Results

  

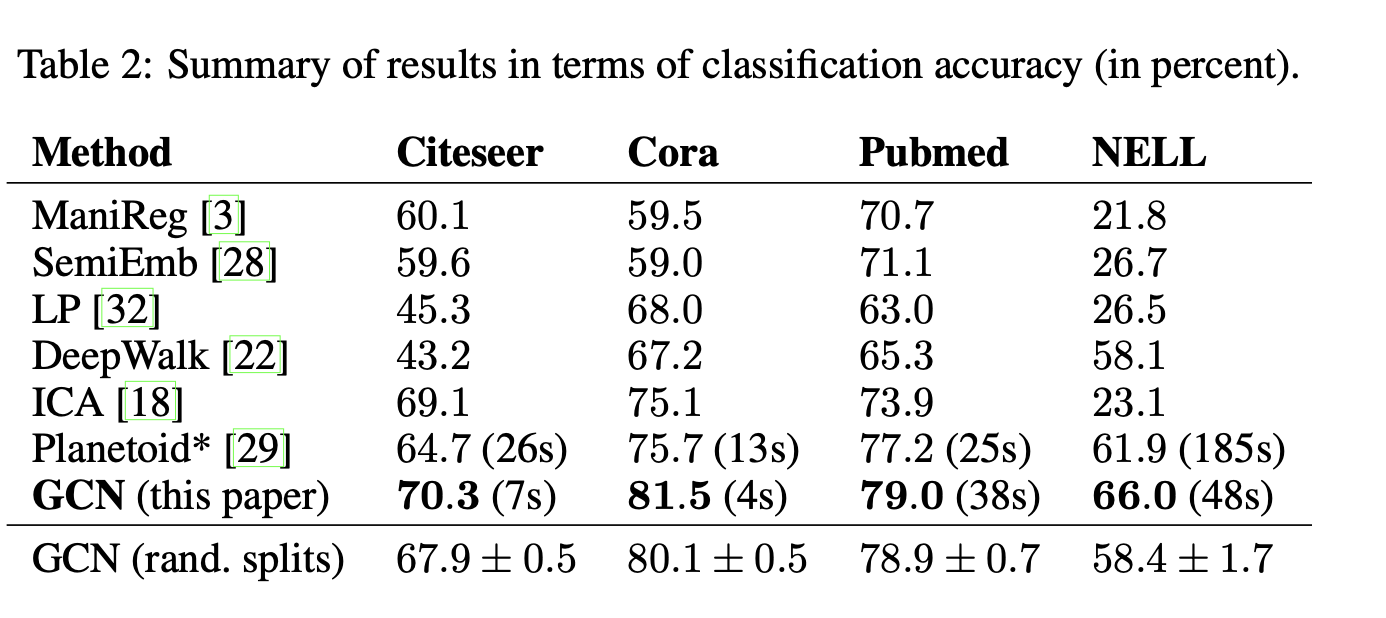
• Propagation function에 따른 ablation