[OD] DEFORMABLE DETR: Deformable Transformers for End-to-End Object Detection
[OD] DEFORMABLE DETR: Deformable Transformers for End-to-End Object Detection
- paper: https://arxiv.org/abs/2010.04159
- github: https://github.com/fundamentalvision/Deformable-DETR
- downstream task: OD
1. Motivation
-
DETR의 느린 학습 속도, feature의 제한된 resolution 사용 이슈를 해결
-
10x less training time
-
sparse sampling attention map생성
2. Contribution
- Deformable convolution기반 best sparse sampling하는 Deformable attention module을 제안함
- Simple & effective한 iterative bounding box refinement mechanism 제안
- DETR 대비 10x 빠른 속도로 더욱 좋은 성능을 냄
-
3. Deformable DETR
-
Original DETR
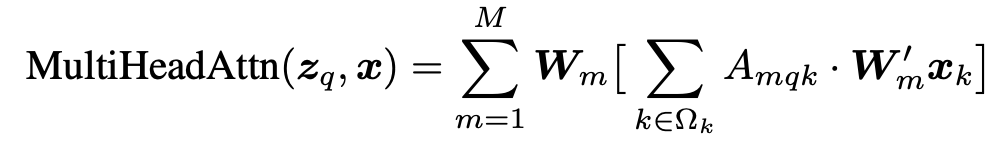
-
W$_m$, W$’_m$: $\mathbb{R}^{C_v \times C}$, learnable weights ($C_v=C/M$)
-
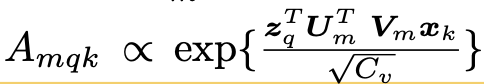
- U$_m$, V$_m$: $\mathbb{R}^{C_v \times C}$, learnable weights
- $\Sigma_{k \in \Omega_k}A_{mqk}=1$
-
Computational Cost: $O(N_qC^2+N_kC^2+N_qN_kC)$
- $U_mz_q, V_mx_k$ = zero mean, 1 std
- Initialize at $A_{mqk} = \frac{1}{N_k}$
-
Encoder
- self-attention complexity: $N_q=HW, N_k=HW, N_v=HW \to O(H^2W^2C)$
-
Decoder
- self-attention complexity: $N_q=N, N_k=N, N_v=N \to O(2NC^2+N^2C)$
- cross-attention complexity: $N_q=N, N_k=HW, N_v=HW \to O(HWC^2+NHWC)$
-> spatial resolution 에 quadratic하게 complexity가 증가함
3.1 Deformable DETR
-
Diagram
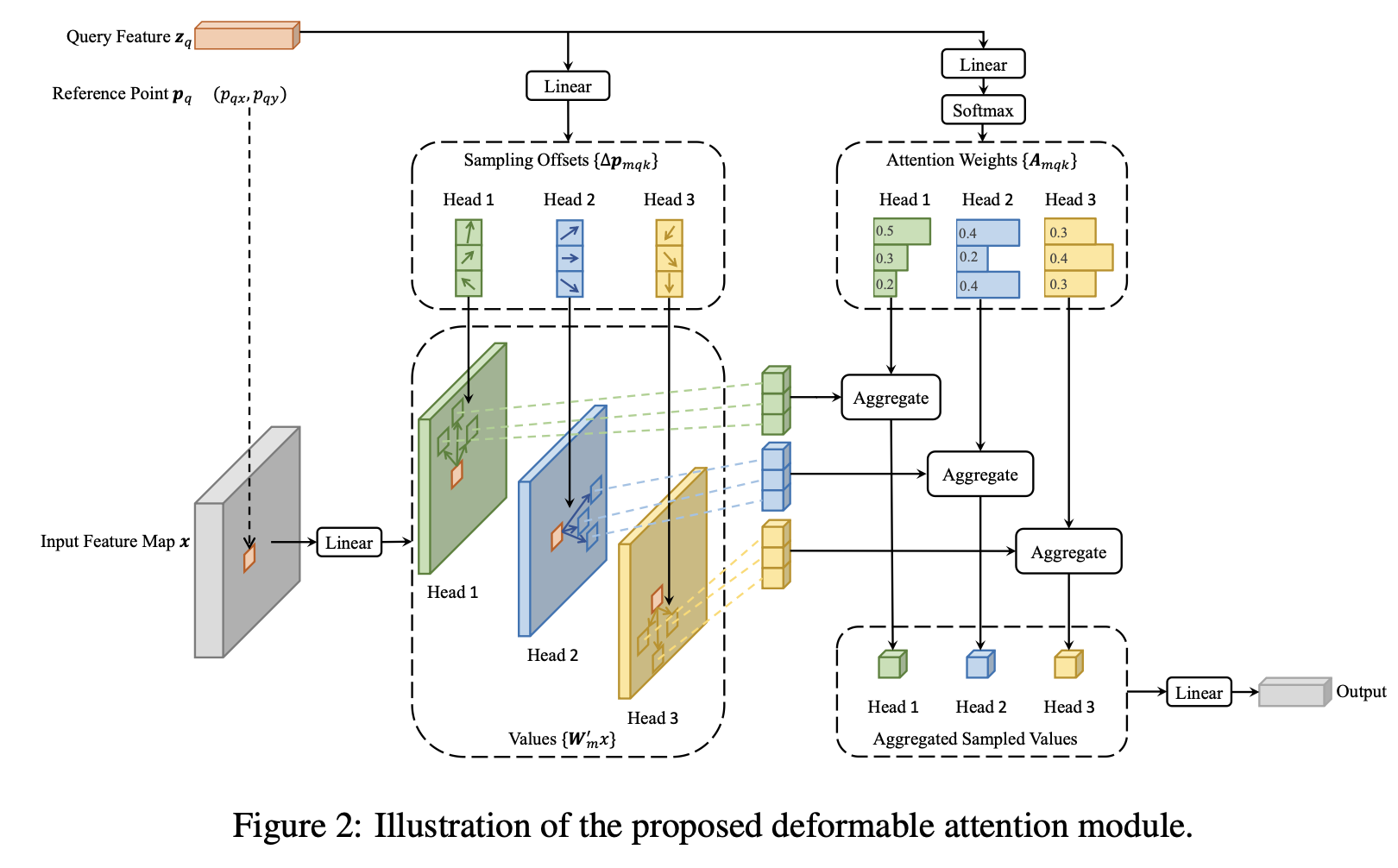
-
Equation
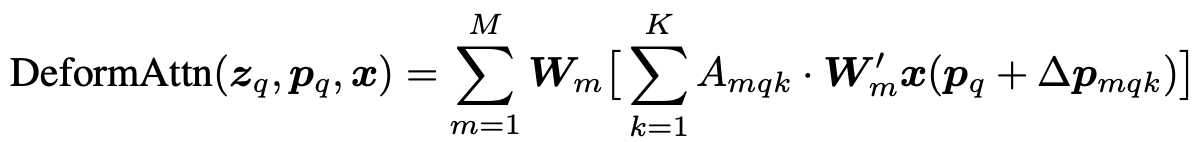
-
p$_q$: 2-Dim real numbers, $ \in \mathbb{R}^2$, object query로부터 linear projection해서 embedding
-
complexity: $O(2N_qC^2+min(HWC^2, N_qkC^2))$
-> spatial resolution에 무관함
-
-
Multi-Scale Deformable Attention
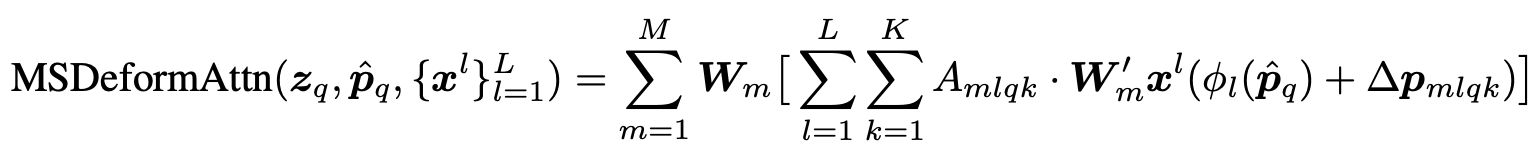
- $M,K,L$: multi-head 갯수, Key-point 갯수, Layer 갯수
-
Decoder의 Self-attention은 그대로 두고, Cross-attention layer만 deformable attention module로 교체
-
Initialization
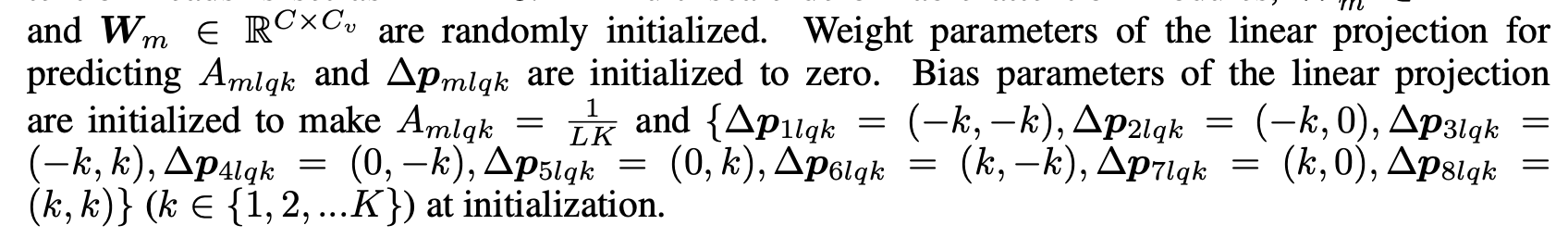
3.2 Iterative Bounding Box Refinement

3.3 Two-stage Deformable DETR
-
3FFN layer로 구성되어 box regression하고, deformable detr의 decoder object query의 입력을 생성해줌
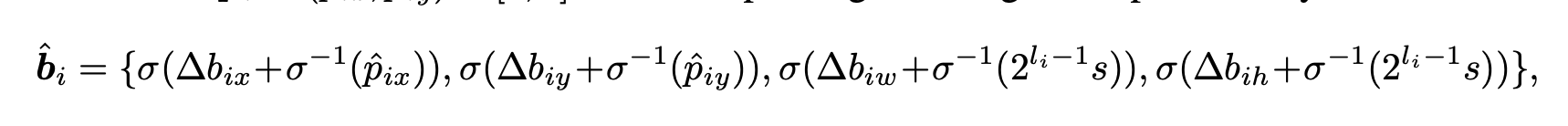
-
4. Experiments
-
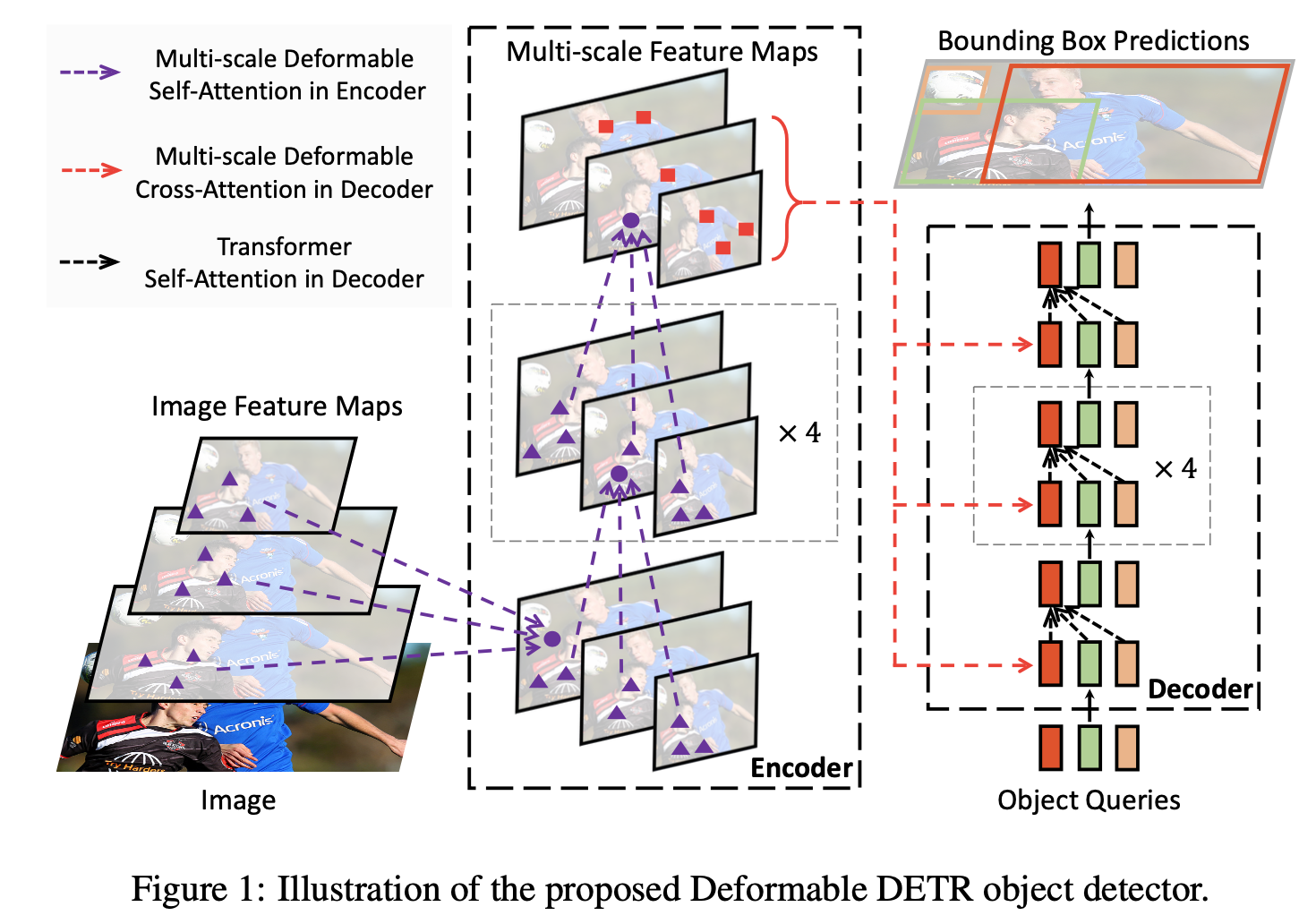
MS COCO vs. DETR
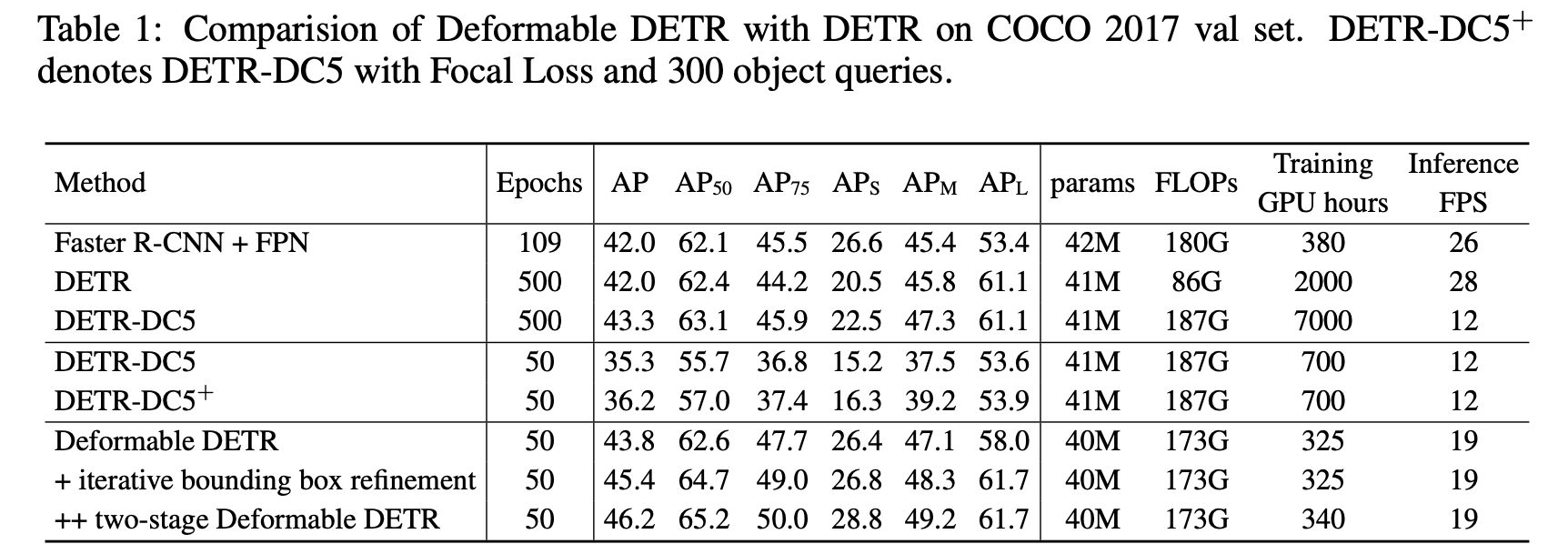
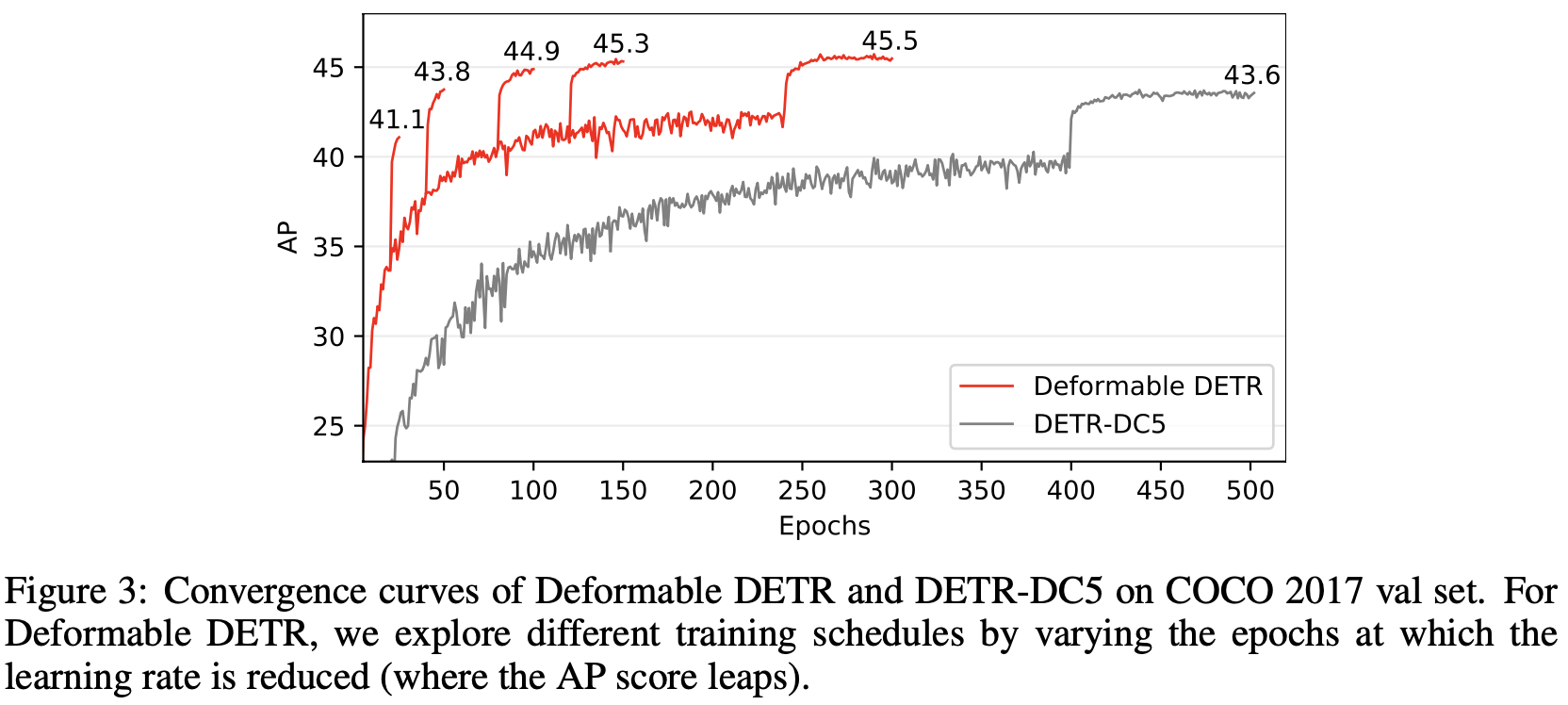
-
Ablation Studies
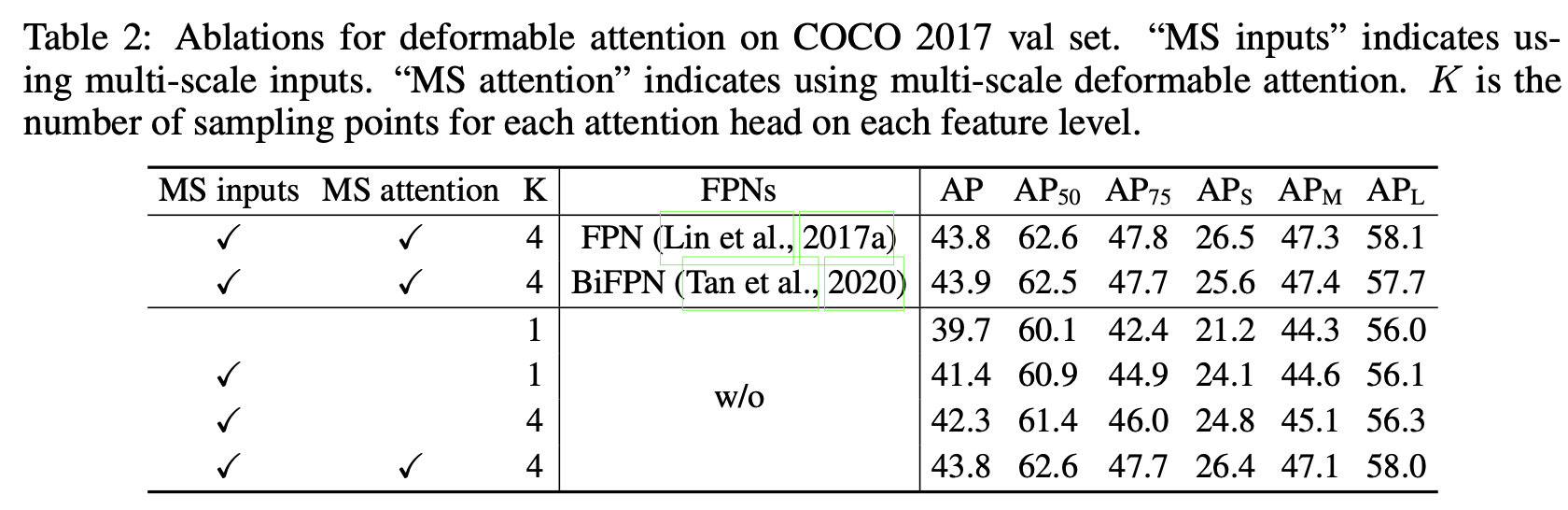
- FPN의 유무에 따른 성능 차이가 없음. 이는 attention에서 이미 cross-level 이 적용되었기 때문.
-
MS-COCO vs. SOTA