[DG][CLS] Domain Generalisation via Domain Adaptation: An Adversarial Fourier Amplitude Approach

---

title: “[DG][CLS] Domain Generalisation via Domain Adaptation: An Adversarial Fourier Amplitude Approach”

---

[DG][CLS] Domain Generalisation via Domain Adaptation: An Adversarial Fourier Amplitude Approach

• paper: https://arxiv.org/pdf/2302.12047.pdf

• ICLR 2023 accpeted (‘23.10.14 인용수 : 3회)

• downsteram task : DG for classification

• contribution

  • “unseen” target domain → “worst-case” target domain 을 synthesis (생성)하여 adaptation 수행.
  • Systhesis를 위해 Fourier Transform으로 주파수 영역으로 변환된 이미지 사용
    • Amplitude : Style에 해당. Generate하는 generator 필요 → MCD (Marginal classifier discrepancy) Loss를 통해 추가적인 classifier없이 worst-case target domain 이미지 생성 가능
    • Phase : Content Semantic 정보를 포함. Source 에서 가져옴
      • Bayseian Modeling을 통해 Adversarial MCD Loss를 구현
  • DG benchmark “DomainBed”에서 SOTA

• key word

  • Domain alignment
  • Data synthesis

• Overall Diagram

  

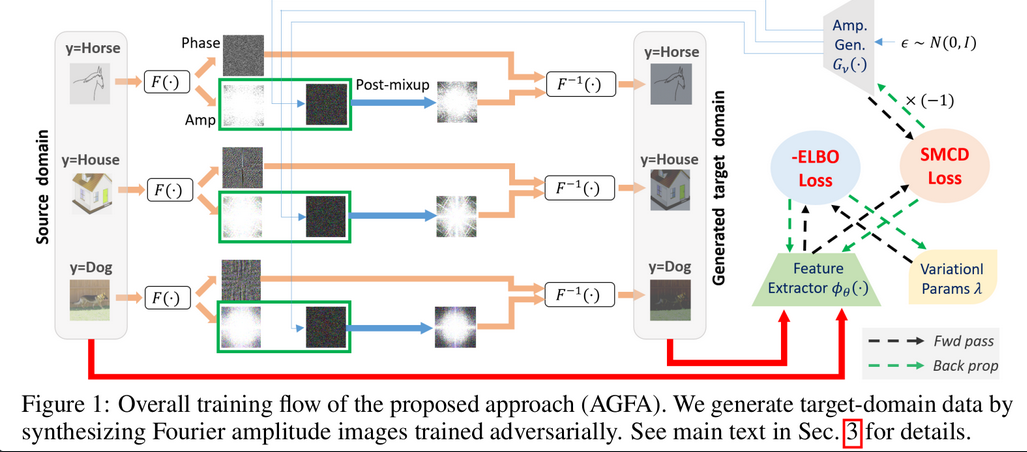
• Constrained MCD Loss의 등장 배경

  • Original MCD Loss : Target domain error의 upper bound를 3가지 텀으로 정의

    

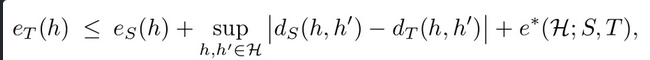
    • h, h’ : Hypothesis space H에 정의된 classifier 모델의 집합의 임의의 서로 다른 classifer

    • sup : supremum

    • S,T : Source domain

      Target domain

    • $d_S, d_T$ : discrepancy of source, discrepancy of target

      

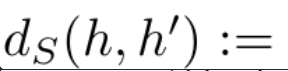
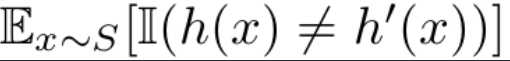
    • $e_S, e_T$ : error rate of source, error rate of target

      

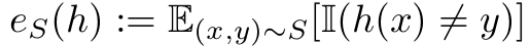
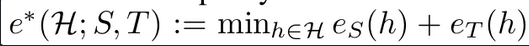
  • constrained MCD Loss : Source error가 작은 상황에서 위 식을 단순화

    

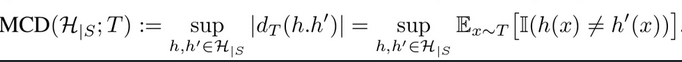
    • $e_s$ ~= 0, $d_s$ ~= 0
    • e*은 뒤에서 설명

• AGFA (Adversarial Generation of Fourier Amplitude)

  • Hypothesis space H 로 정의된 set에 속한 model h에 대해 구현 ( individual h x)

    

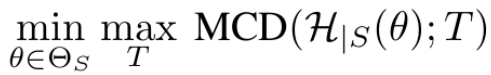
  • 위 space를 정의하기 위해 Bayesian linear classifier + deterministic feature extractor 사용

    

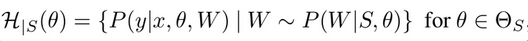
    • $w_j$: j번째 class head (stochastic)
    • $\phi_theta$ : feature extractor (deterministic)

  • Optimizing worst-case target domain

    

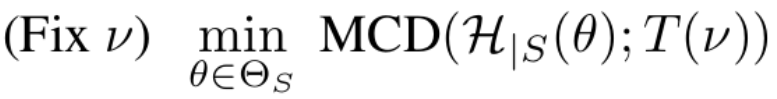
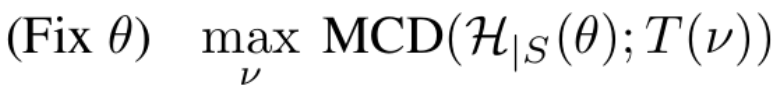
    • T: target domain Generator

  • Algorithm Summary

    • nu : parameters for generator T
    • theta : parameters for classifier h

• Target domain 생성 flow

  

• Variational Inference를 통한 Source-confined Hypothesis 구현

  • P(W	S,theta)를 직접 구하기 어려우므로 Gassian variational density로 근사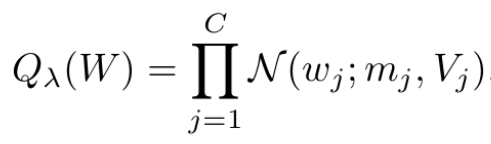

    

  • Elbo 를 사용해서 Q_lambda ~= P(W

    S, theta)가 되도록 학습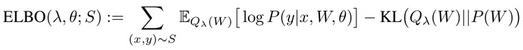

    

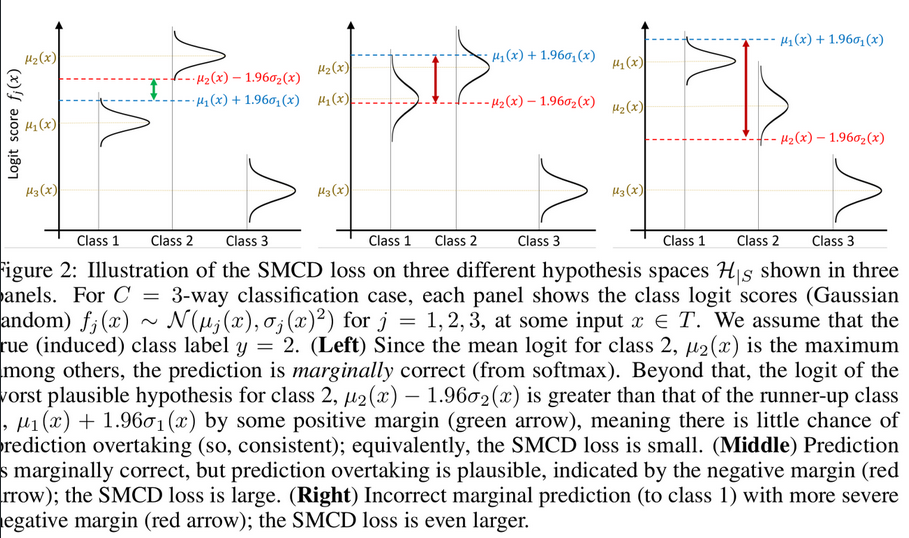
• MCD Loss 최적화

  

  • Top1 class score의 marginal min score 값이 Top2 class score의 max marginal score보다 높아지도록 학습

    

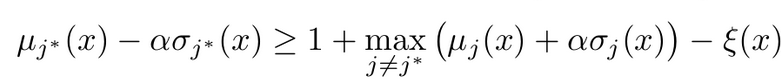
    • $\mu_j, \sigma_j$ : Top1의 평균, 분산
    • $\mu_j, \sigma_j$ : Top2의 평균, 분산
    • slack variable : 0이상의 임의의 hyperparameter. (margin에 해당)
    • 1 : normalization을 위해 추가. 제거 시, mu & sigma가 너무 작아진다고 함.

  • MCD Loss 최종 식

    

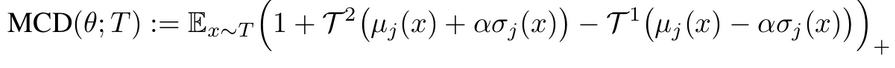
    • $T^1, T^2$: Top1, Top2
    • + : 최소가 0이되도록 하는 함수 (ReLU)

• Supervised MCD Loss

  • Target domain의 semantic은 source에서 오므로, source label 사용 가능 → supervised learning!

    

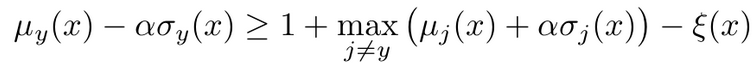
    • 마지막 세번째 SMCD항을 통해 e*=e_T 이 줄어듦

• Overall Algorithm Summary

• 추가 고려사항

  • Amplitude Mixup : 이를 안하면 semantic이 해친다고 함

    

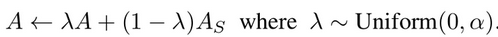
• Overall Algorithm Summary

• 추가 고려사항

  • Amplitude Mixup : 이를 안하면 semantic이 해친다고 함